Омическое сопротивление, включенное в цепь переменного
тока, становится по величине несколько больше, чем в цепи постоянного тока. Это
объясняется явлением поверхностного эффекта (скин-эффект). Оно заключается в
том, что переменный ток вытесняется к наружным слоям проводника, что
равносильно уменьшению сечения и увеличению сопротивления (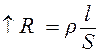 ). Внутренние части проводника окружены
большим изменяющимся магнитным потоком Ф, имеют большую противо–эдс
самоиндукции и проводят меньший ток. Однако, явление поверхностного эффекта
значительно сказывается только на очень высоких частотах, типа радио частот.
). Внутренние части проводника окружены
большим изменяющимся магнитным потоком Ф, имеют большую противо–эдс
самоиндукции и проводят меньший ток. Однако, явление поверхностного эффекта
значительно сказывается только на очень высоких частотах, типа радио частот.
Омическое сопротивление в цепях переменного тока называется активным (r): только в нем происходит преобразование электрической энергии в другие виды (например, в тепло).
Рассмотрим цепь переменного тока, содержащую только одно активное сопротивление r (рис. 3.5).
|
|
Пусть приложенное
напряжение синусоидально, (рис. 3.6 а) т.е.:
![]() .
(3.10)
.
(3.10)
Тогда по закону Ома:
![]()
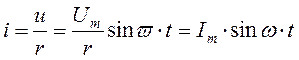 .
(3.11)
.
(3.11)
В равенстве (3.11) обозначено:
Рис. 3.5 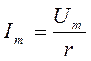 . (3.12)
. (3.12)
Это закон Ома для амплитудных значений тока и напряжения.
Поделив обе части равенства (3.12) на ![]() , получим:
, получим:
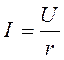 ,
(3.13)
,
(3.13)
т.е. закон Ома для действующих значений. Векторная диаграмма показана на рис. 3.6 б.
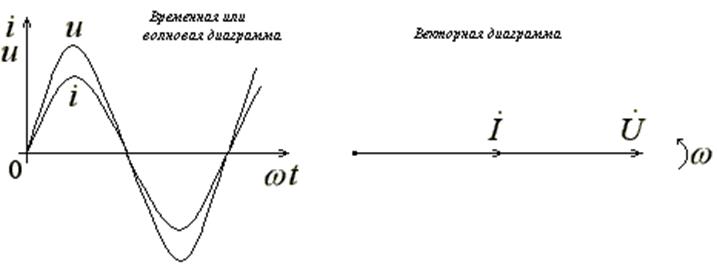
(а) (б)
Рис. 3.6
Сравнивая равенства (3.10) и (3.11) видим, что ток и
напряжение в цепи совпадают по фазе, т.е. ![]() .
.
3.5. Цепь, содержащая только индуктивность
Это идеализированный случай, ибо обычная катушка индуктивности всегда имеет какое-то активное сопротивление.
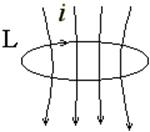 Пусть имеется контур L, который
пронизывается магнитным потоком Ф. Если поток меняется во времени,
т.е. Ф = Ф(t), то в
контуре наводится эдс
(рис. 3.7):
Пусть имеется контур L, который
пронизывается магнитным потоком Ф. Если поток меняется во времени,
т.е. Ф = Ф(t), то в
контуре наводится эдс
(рис. 3.7):
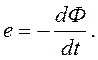
![]() (3.14)
(3.14)
Под действием ее в замкнутом контуре потечет ток i. Если
Рис. 3.7
контур сложный, например, содержит несколько витков, то вводят понятие потокосцепления:
![]()
![]() (3.15)
(3.15)
где wk – часть витков контура, сцепленных с определенным потоком Фk. Тогда закон электромагнитной индукции для любого сложного контура запишется в прежней форме:
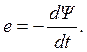 (3.16)
(3.16)
Потокосцепление
![]() может быть вызвано током i
в самом контуре, при этом оказывается, что
может быть вызвано током i
в самом контуре, при этом оказывается, что ![]() - т.е.
- т.е. ![]() ,
откуда
,
откуда 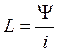 - называется
индуктивностью. Её размерность: [
- называется
индуктивностью. Её размерность: [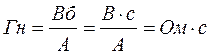 ].
].
Потокосцепление ![]() ,
связанное с первым контуром, может быть вызвано током i
во втором контуре. При этом опять оказывается, что
,
связанное с первым контуром, может быть вызвано током i
во втором контуре. При этом опять оказывается, что ![]() . Откуда:
. Откуда:
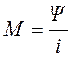 ,
(3.17)
,
(3.17)
называется взаимной индуктивностью [Гн]. Рассмотрим цепь переменного тока, содержащую только индуктивность L (рис. 3.8)
|
|
Пусть ![]() , согласно (3.16) эдс
, согласно (3.16) эдс
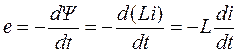 .
(3.18)
.
(3.18)
По второму закону Кирхгофа: 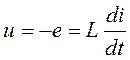 ,
,
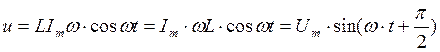 . (3.19)
. (3.19)
Рис. 3.8
В равенстве (3.19) обозначены:
![]() , (3.20)
, (3.20)
где ![]() - индуктивное сопротивление.
- индуктивное сопротивление.
Поделив (3.20) на ![]() , получим
закон Ома для действующих значений:
, получим
закон Ома для действующих значений:
![]() .
(3.21)
.
(3.21)
Размерность хL – Ом,
[ωL]=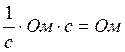 ,
,
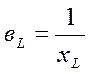 - индуктивная проводимость, [См].
- индуктивная проводимость, [См].
Волновые (а) и векторная (б) диаграммы показаны на рис. 3.9.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.