Расчет электрических цепей: Учебное пособие для студентов, изучающих дисциплины «Электротехника и электроника», «Общая электротехника», «Теоретическая электротехника», страница 18

Так, вектор  стрелкой направлен к точке "а" (рис. 4.9). Это произошло потому, что имеет смысл поддерживать аналогию с постоянным током, где

                    U_ав= j _а- j_в.                                           (4.9)

Для фазных и линейных ЭДС соотношения аналогичны (4.8).  

                       Рис. 4.9                   

       

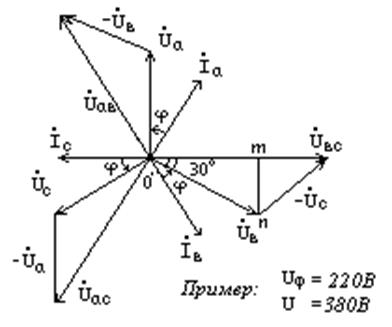
Для симметричной системы имеем:

U_а = U_в = U_с = U_ф ,

I_a = I_в = I_с = I_ф,

I₀ = 0,

j_а = j_в = j_с = j.

Построим векторную диаграмму для симметричной системы согласно (4.8) (рис. 4.10).

Из Dо' mn следует:0'm=0'ncos 30⁰

,

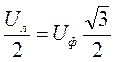U_л =U_ф ,

U=U_ф,      I=I_ф,            I₀=0.                                         Рис. 4.10

4.4.  Соотношения между линейными и фазными величинами

напряжений и токов при соединении треугольником

При соединении треугольником (рис. 4.11) фазные и линейные напряжения равны:

Рис. 4.11

(4.10)

Аналогичное заключение можно сделать для фазных и линейных ЭДС.

По I закону Кирхгофа для узлов а; в; с имеем:

I_а + I_{с а}= I_ав,I_а = I_{а в} - I_са,

I_в + I_ав = I_вс,                    I_в = I_вс  - I_ав,                                                        (4.11)

                                                                   I_с + I_вс = I_са                                 I_с = I_са  - I_вс.

Линейные токи равны  геометрической разности соответствующих фазных токов.                                                                                                            

Покажем (4.11) на векторной диаграмме (рис. 4.12).

Для симметричной системы имеем:

U_ав = U_вс = U_са = U_ф = U,

I_ав = I_вс = I_са = I_ф,

j_ав = j_вс = j_са = j.

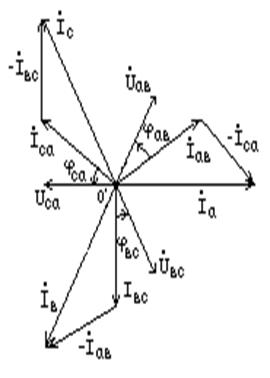
Построим векторную диаграмму для симметричной системы по (4.11)     (рис. 4.13).                                                      

     Рис. 4.12                                                                                         Рис. 4.13

Из D omn (рис. 4.13) следует: om=oncos30⁰         или

I =.

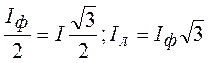4.5.   Расчет симметричных трехфазных цепей

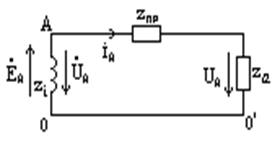Если в этом случае источник и приемник энергии соединен , то расчет сводится к расчету однофазной цепи. Возьмем, например фазу А.

Дано: или , , .

Определить: , _.

Решение:

Т.к. в симметричной системе I₀=0, то ==0, Рис. 4.14                    точки 0 и 0' можно соединить накоротко, как

имеющие одинаковый потенциал (рис. 4.14). Тогда:

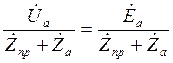=.                                                         (4.12)

                             =              _.                                                                                                              (4.13)

Положение векторов    и   найдется поворотом соответствующих для фазы А на угол (-), а векторов    и _с  - на угол (+). Величины же Е; U; I останутся такими же. Если приемник энергии соединен D, то лучше всего заменить его эквивалентной , найти, как указано выше, линейные токи, затем фазные для  D (делением на Ö3) и только после этого напряжение приемника.

4.6.  Расчет несимметричных трехфазных цепей

Является более трудной задачей и ведется для каждой фазы в отдельности. Можно выделить 4 характерных случая расчета.

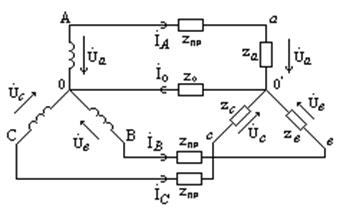
А. Приемник соединен , имеется нулевой провод, заданы фазные напряжения источника (рис. 4.15).

Дано:

,,, ,, , _{, .}

Определить:

_{, , , ,}

 , ,  , _.

Рис. 4.15

а) Вычисляем сопротивления и проводимости фаз и нулевого провода:

, =,       =,

                                       ,  = ,                                    ,         = .

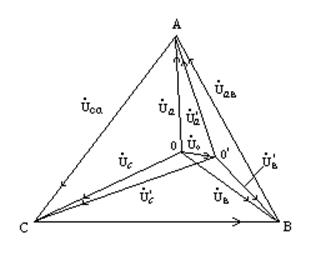б) Строим топографическую диаграмму напряжений источника и приемника (рис. 4.16).

₀ = ₀₀ ¹ 0, поэтому точка 0'  не совпадает с 0. Положение 0' пока определим произвольно внутри DАВС. Тогда сразу получим вектора , ,  – напряжение приемника с учетом сопротивлений линейных проводов (т.е. oт 0' до  А, В, С  соответственно).

Из диаграммы следуют соотношения:

                                                                                                                                                                                  Рис. 4.16                    ; ;            (4.15)

в) Определим  по методу 2-х узлов: