Расчет электрических цепей: Учебное пособие для студентов, изучающих дисциплины «Электротехника и электроника», «Общая электротехника», «Теоретическая электротехника», страница 16

 где  - полное комплексное сопротивление, где

х = x_L-x_C – реактивное сопротивление;

х > 0,  если x_L > x_C;   x<0,  если  x_L < x_C.

Пример:  - преобладает емкостное сопротивление.

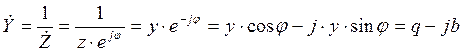                 - полная комплексная проводимость, где

b= b_L - b_C  – реактивная проводимость;

b> 0,  если  b_L  >b_C;  b< 0,  если  b_L  <  b_C.

Пример:  - преобладает емкостная проводимость.

2.  Законы Кирхгофа

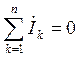                                        - 1-й;  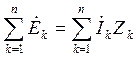              - 2-й.

Запись основных законов (Ома и Кирхгофа) в символическом методе по форме не отличается от записи таковых для цепей постоянного тока, только здесь вещественные числа заменены комплексными.

Это позволяет при пользовании символическим методом применять к расчету цепей переменного тока все ранее известные способы для цепей постоянного тока (наложения, контурных токов, 2-х узлов, законов  Кирхгофа и т.д.).

Особенно удобно вычисляется символическим методом мощность электрических цепей.

Пусть в цепи известны напряжение  и ток . Запишем сначала сопряженный комплекс тока  и вычислим произведение:

- получилась комплексная полная мощность .

- активная мощность,

- реактивная мощность,

[ВА] - полная мощность.

Пример:

	P = 160 Вт;  Q = 120 ВАр;        S=200 ВА.
P, Q, S - ?

4. ТРЕХФАЗНЫЕ ЦЕПИ ЭЛЕКТРИЧЕСКОГО ТОКА

4.1.  Основные понятия

В настоящее время электрическая энергия производится, передается, распределяется и потребляется практически исключительно как энергия трехфазного переменного тока.

Это объясняется рядом преимуществ  трехфазного тока по сравнению с другими системами.

Основные преимущества:

1.  Возможность получить наиболее качественное вращающееся магнитное поле, необходимое для двигателей переменного тока, прежде всего для асинхронных и синхронных.

2.  Экономичность генераторов, трансформаторов, электродвигателей и ЛЭП, выполненных на трехфазном токе.

Трехфазные цепи являются частным случаем цепей многофазных – случаем наиболее простым и универсальным.

Система трехфазного переменного тока, включая сюда теоретические разработки и практическое выполнение в металле трехфазного генератора, трансформатора, ЛЭП и трехфазного АД, была создана в 1888-91 гг. русским ученым и инженером М.О. Доливо-Добровольским.

Познакомимся вначале с основными определениями для  3х-фазных систем.

Трехфазной цепью называют совокупность трех однофазных цепей, в которых действуют три ЭДС одной и той же частоты, но отличающиеся по фазе.

Отдельные цепи, составляющие трехфазную цепь, называют ее фазами.

Трехфазная цепь называется симметричной, если равны амплитуды ЭДС, сдвиг по фазе между ними составляет угол ( 120 ⁰ ), а сопротивления всех фаз А, В, С одинаковы по величине и характеру, т.е. они равны как комплексы:

Покажем принципиальное получение трехфазного тока на простейшей модели (рис. 4.1).

В равномерном магнитное поле вращается против часовой стрелки с угловой скоростью  система из 3-х одинаковых катушек, расположенных соосно под углом 120 ⁰  друг к другу (рис. 4.1).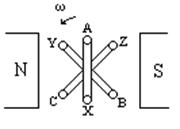         

       В катушках будут индуктироваться синусоидальные ЭДС, сдвинутые во времени, или по фазе, на угол . При                                  Рис.4.1           этом частота  и амплитуды этих ЭДС будут одинаковы.

В этом случае говорят, что ЭДС образует симметричную трехфазную систему. Их мгновенные значения могут быть записаны как:

i=E_msinωt,

i=E_msin(ωt–),                                                                     (4.2)

i=E_msin(ωt-)=E_msin(ωt +).

Равенству (4.2) соответствуют временная диаграмма (рис. 4.2) и векторная диаграмма (рис. 4.3).

                                              

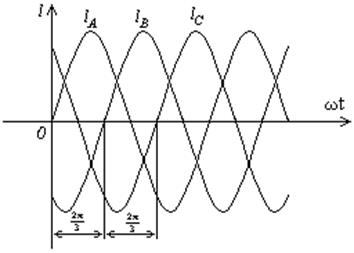
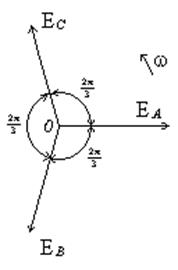
Рис. 4.2                                                                  Рис. 4.3

Если к каждой катушке присоединить одинаковые комплексные сопротивления, то под действием ЭДС в каждой цепи потекут токи, которые будут составлять симметричную систему токов.

Ее аналитическая запись, временная и векторная диаграммы будут аналогичны приведенным для ЭДС, но только надо учитывать угол сдвига  между ЭДС и током.