Сложную систему уравнений надо решать с помощью определителей
Ik=![]() ,
,
или иным математическим способом.
2.2 Метод контурных токов
Для сложных цепей, содержащих более 2-х узлов, метод контурных токов является наиболее простым и универсальным, ибо он значительно сокращает число уравнений по сравнению с непосредственным применением законов Кирхгофа. Впервые предложен Максвеллом.
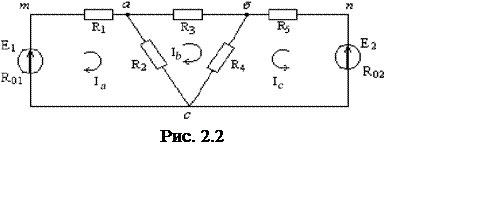
Для примера рассчитаем сложную цепь предыдущего раздела.
Сущность метода заключается в том, что сложная цепь рассматривается как совокупность соприкасающихся ячеек или контуров (отличие от независимых контуров предыдущего метода).
![]()
![]() Каждой ячейки
приписывается некоторый контурный ток произвольного направления, а ток в общей
ветви находится, как алгебраическая сумма контурных токов (рис. 2.2). При
таком условии I-й закон
Кирхгофа удовлетворяется автоматически и составлять по нему уравнение не надо (
Каждой ячейки
приписывается некоторый контурный ток произвольного направления, а ток в общей
ветви находится, как алгебраическая сумма контурных токов (рис. 2.2). При
таком условии I-й закон
Кирхгофа удовлетворяется автоматически и составлять по нему уравнение не надо (![]() Iк = 0, превращается
в тождество 0 = 0).
Iк = 0, превращается
в тождество 0 = 0).
Однако, при составлении уравнений по II закону Кирхгофа нужно помнить одну особенность. Алгебраическая сумма ЭДС каждой ячейки равна алгебраической сумме произведений:
а) контурного тока данной ячейки на сумму сопротивлений всех ветвей этой ячейки;
б) контурных токов всех ячеек, смежных с данной, на соответствующие сопротивления общих ветвей. Правило знаков ЭДС и токов остается прежним, причем контур обходится в направлении собственного контурного тока.
![]()
![]() Ia (R01+R1+R2)-IbR2=E1, Iста=Ia,Iас=Ia–Ib,
Ia (R01+R1+R2)-IbR2=E1, Iста=Ia,Iас=Ia–Ib,
Ib (R2+R3+R4)–IaR2+IcR4=0, Iав=Ib,Iбс=Ib+Ic, (2.1)
Ic (R02+R5+R4)+IbR4=E2. Iспб=Ic.
Токи во внешних ветвях цепи равны соответствующим контурным, в общих ветвях – их алгебраическая сумма [5]. Число ячеек всегда значительно меньше числа ветвей, отсюда число уравнений в системе меньше, чем при непосредственном применении законов Кирхгофа (3 вместо 5 в приведенном примере).
Сложную систему уравнений лучше решать с помощью определителей.
2.3. Метод двух узлов
Если сложная цепь имеет много параллельных ветвей, но всего два узла, то самым простым оказывается метод двух узлов.
Пусть имеется расчетная схема (рис.2.3):
Запишем I закон Кирхгофа для узла а: ![]() Ik
= 0. (2.2)
Ik
= 0. (2.2)
По закону Ома для активного участка цепи:
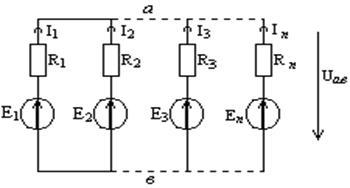 Ik=
Ik=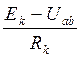 =(Ek – Uав)qк. (2.3)
=(Ek – Uав)qк. (2.3)
Подставляя (2.2) в (2.3), получим
(рис. 2.3):
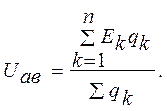
![]() (Ek
– Uав)qк
=0, (2.4)
(Ek
– Uав)qк
=0, (2.4)
Рис. 2.3
откуда:
Определив Uав, находят токи в ветвях по формулам (2.3).
В отношении формул (2.3) и (2.4) следует сделать замечания:
1). Если ветвь не содержит ЭДС, то в соответствующей ветви Ек = 0, а проводимость qк остается.
2). ЭДС обратного направления войдет в формулы со знаком минус.
3). Если окажется Ек < Uав, то в формуле (2.3) соответствующий ток получится отрицательным, т.е. будет направлен против своей ЭДС.
2.4. Метод наложения
Применим только для линейных цепей. Является частным случаем принципа наложения, суть которого заключается в независимости действия источников энергии (доля тока в нагрузку от источника не меняется, есть ли соседние источники или их нет).
По этому методу сложную схему разбивают на ряд простых, в каждой из которых действует лишь один источник, для остальных источников ЭДС приравнивается нулю (Ек = 0), но их внутренние сопротивления остаются. Токи в ветвях каждой простой схеме называются частичными.
Действительные токи в ветвях исходной схемы находятся алгебраическим суммированием частичных токов.
Рассмотрим метод на следующем примере (рис. 2.4).
|
|
|
1 схема: Е2 = 0
|
|
2 схема: Е1 = 0
|
Введем следующие обозначения, облегчающие применения формул Поливанова
R1 = R01 + R¢1, R2 = R02 + R¢2,
åRiRk = R1R2 + R2R3 + R3R1,
I¢2
= 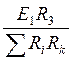 , I¢3 =
, I¢3 = 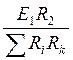 ,
,
I¢1
= I2 +
I3 = 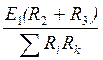 ,
,
I¢¢3 = 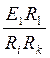 ; I¢¢1 =
; I¢¢1 = 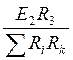 ,
,
I¢¢2 = I¢¢3 + I¢¢1 = E2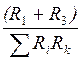 .
.
Исходная расчетная схема
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.