Рис. 3.2
3.2 Среднее и действующее значения синусоидального тока
Т.к. среднее значение синусоидальной величины за период равно нулю, то говорят о среднем значении синусоидального тока за Т/2 (рис. 3.3)
Если, например:
,
то:
.
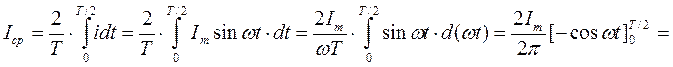
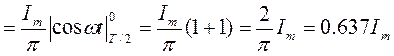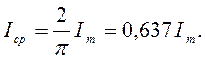(3.6)
|
|
Приборы магнитоэлектрической системы показывают среднее значение выпрямленного переменного тока.
Аналогично (3.6) выражается Ucp и Ecp.
Действующим значением переменного тока называется среднее квадратичное значение тока за период, т.е.:
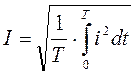. (3.7)
Рис. 3.3
Если: 
,
то:
, 
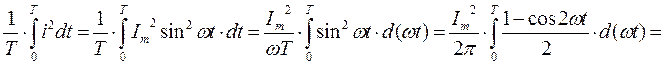
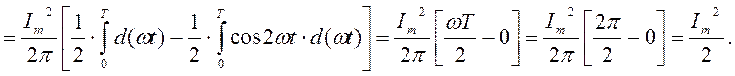
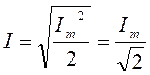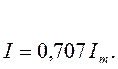(3.8)
Аналогично определяется действующее значение напряжения U и эдс Е.
Вводится так же понятие коэффициента формы:
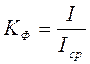; для синусоиды 
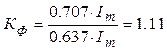. (3.9)
Понятие действующего значения переменного тока связанно с тепловым и механическим действиями тока, которые пропорциональны квадрату тока.
В этом смысле действующее значение переменного тока равняется такому постоянному току, который за время, равное периоду Т, выделяет в сопротивлении такое же количество тепла, что и данный переменный ток. Действующее значение тока или напряжения – наиболее важная и широко применяемая характеристика переменного тока.
Вольтметры и амперметры переменного тока устроены так,
что в большинстве случаев непосредственно показывают действующее значение
напряжения и тока (пример с электрической сетью 380/220 В; 
(В).
3.3. Векторные диаграммы
Если электрические величины в цепи ( i, u, e) синусоидальны и имеют одинаковую частоту ω, то алгебраические операции над ними значительно упрощаются введением векторных диаграмм. В основе построения этих диаграмм лежит то обстоятельство, что любая синусоидальная величина может быть представлена вращающимся вектором. Длина этого вектора равна амплитуде синусоидальной величины. Если вращать такой вектор против часовой стрелки с угловой скоростью ω и вести отсчет углов от горизонтальной оси, то проекция вектора на вертикальную ось дает мгновенное значение синусоидальной величины (рис. 3.4):
.
|
|
При построении векторных диаграмм вводят следующие упрощения
1). Опускают годографы вращающихся векторов и координатной оси.
2). Начальный или исходный вектор берут с любой начальной фазой, даже равной нулю, а остальные вектора окажутся сдвинутыми относительно исходного на углы равные
Рис. 3.4
соответствующим разностям фаз, причем углы при вращении диаграммы изменяться не будут.
3). Т.к. e, u, i – скалярные величины, то соответствующие им вектора не будут физическими, а будут условными, символическими, и для отличия от физических, будут обозначаться символом с точкой, а не чертой наверху, например Ė, Ů, İ.
4). Обычно диаграмма строится не для амплитуд, а для действующих значений, как наиболее часто применяемых в расчетах.
Итак, векторная диаграмма – это совокупность векторов электрических величин, отражающая процесс в электрической цепи и построенная с учетом правильной ориентации векторов друг относительно друга.
Если векторная диаграмма для напряжений строится в той же последовательности, в какой ток обтекает элементы цепи (Z, L, C), то такая диаграмма называется ТОПОГРАФИЧЕСКОЙ.
Она обладает важным преимуществом: расстояние между двумя любыми точками на диаграмме в масштабе равно напряжению между теми же точками реальной цепи.
Для точных аналитических расчетов обычно символ вектора токов и напряжений заменяют комплексными числами, которые можно записать в трех формах: алгебраической, тригонометрической и показательной; в зависимости от производимой операции берут наиболее удобную форму.
3.4. Цепь, содержащая только активное сопротивление
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
