Расчет электрических цепей: Учебное пособие для студентов, изучающих дисциплины «Электротехника и электроника», «Общая электротехника», «Теоретическая электротехника», страница 10

                                      (а)                                                          (б)

                                                      Рис. 3.9

Из (3.19) и рис. 3.9 видим, что напряжение в такой цепи опережает ток по фазе на угол π/2, т.е. .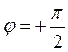

3.6.  Цепь, содержащая только емкость С

Металлические пластины, разделенные слоем диэлектрика, способны накапливать электрические заряды разных знаков, если их присоединить к источнику напряжения. При этом заряд на одной пластине ≡ U.

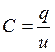  ;  - емкость, 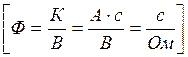,                 Рис. 3.10

мкФ = 10^-6Ф;  нФ = 10^-9Ф;   пФ = 10^-12Ф.

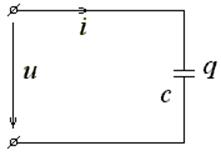
Рассмотрим цепь переменного тока, содержащую только емкость С (рис. 3.11).

Пусть

.                                                           (3.23)

 Тогда:

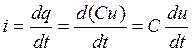                         .                                  (3.24)

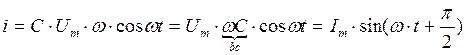(3.25)

                      Рис. 3.11

В равенстве (3.25) обозначены:

 -закон Ома для амплитуд.                                           (3.26)

Деля (3.26) на , получим:

 –закон Ома для действующих значений.                         (3.27)

 - емкостная проводимость [См].

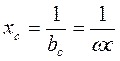 -(реактивное) емкостное сопротивление.

Равенство (3.27) можно также записать:

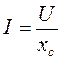                .                                                                                                   (3.28)

Волновые (а) и векторная (б) диаграммы  показаны на рис. 3.12.                                                  

                                    (а)                                                            (б)

                                                            Рис. 3.12                                           

Сравнивая (3.23) и (3.25), видим, что ток в такой цепи опережает напряжение по фазе на угол  π/2, т.е. .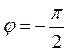

3.7.  Последовательное соединение r, L, C

Пусть .                                   (3.29)

Основываясь на сведениях предыдущих трех параграфов, запишем мгновенные значения напряжений на каждом элементе для схемы, изображенной на рис. 3.13:.

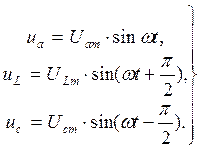                                         (3.30)

               Рис. 3.13  

Амплитуды напряжений:

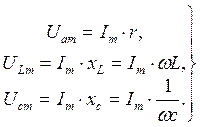                                                                                                (3.31)

Поделив (3.31) на ,  получим:

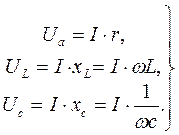                                                     (3.32)

          По II закону Кирхгофа имеем:

                                      (3.33)

В (3.33) все синусоидальные величины заменим вращающимися векторами и перейдем к действующим значениям.

Тогда получим следующее векторное равенство:

.                                                                   (3.34)

Построим векторную диаграмму, соответствующую (3.34), взяв за исходный вектор тока  I  (рис. 3.14).

Из ∆АОВ по теореме Пифагора

имеем:

        ,

       откуда:

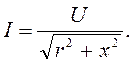                       (3.35)       

     Уравнение (3.35) есть закон Ома в                                                            

                       Рис. 3.14                               общем виде.

В (3.35) обозначены:

r – активное сопротивление цепи;

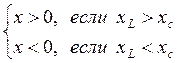x=x_L-x_c – реактивное сопротивление цепи   ;

 - полное сопротивление цепи.

Запишем сопротивление z  в трех формах:

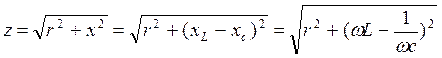                .                                  (3.36)

Вводя понятие z-размер, закон Ома (3.35) можно записать более кратко:

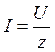                                                          ,                                                           (3.37)

т.е. так же, как в постоянном токе.

Из ∆АОВ определяется угол сдвига  φ:

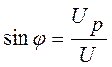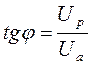                                                    ;   .                                   (3.38)

     Поделив все стороны треугольника напряжений АОВ на величину тока I, получим подобный ему треугольник сопротивлений (рис. 3.15).

Из него так же можно определить φ:

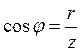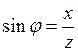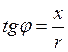; ; .                           (3.39)

Из двух последних формул определяется так же и знак  φ.

На векторных диаграммах знак φ определяется

          Рис. 3.15

автоматически, если условиться отсчитывать его от вектора тока к вектору напряжения по кратчайшему пути (рис. 3.16).