Электротехника \ Электротехника и электроника

Расчет электрических цепей: Учебное пособие для студентов, изучающих дисциплины «Электротехника и электроника», «Общая электротехника», «Теоретическая электротехника», страница 14

; ;

;

.

  Условие идеального резонанса:

,       (3.51)

здесь заменяется другим:

  .

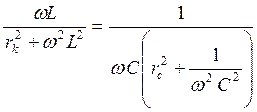            Рис. 3.34

Если при идеальном резонансе токов q≈0, то ,  а  z → ∞. Значит,

 I→ 0. Это свойство используется в фильтрах при устройстве “пробок” для отдельных частот.

3.14.  Частотные зависимости токов и напряжений

А. При последовательном соединении элементов r, L, С  (см. схему идеального резонанса напряжений).

Эти  зависимости  I,  Ua, UL,  UC = f(ω),  0 < ω < ∞  показаны на рис. 3.35.

1) ,

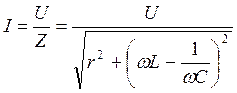ω → 0; I → 0;

ω → ω0; I → Im;

ω → ∞; I → 0.

2) ,

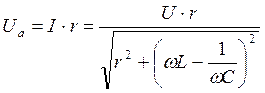           Рис. 3.35                                             Ua(ω) ~ I(ω); ω → ω0;   Ua = U.      

3) ,

ω → 0;          UL → 0;

ω → ω0;        UL = Uc;

ω → ωL;        UL → max;

ω → ∞;          UL →U.

4)

ω → 0;          Uc → U;

ω → ωc;        Uc → max;

ω→ω0;        Uc =UL;

ω→∞;          Uc →0.

Б. При параллельном соединении элементов q, L, С (см. схему идеального резонанса токов).

Это зависимости Ia;  I;  IL;  Ic = f(ω),  причем  0 < ω < ∞  (рис. 3.36).

1)  - прямая, ‌|| горизонтальной оси.

2)  - прямая, проходящая через начало координат.

           Рис. 3.36

3) 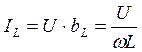- гипербола,

ω→ 0;          IL → ∞;

ω→ ω0;        IL = Ic;

ω→ ∞;          IL → 0.

4)

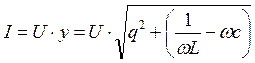
ω→ 0;          I→ ∞;

ω→ ω0;        I→ Ia;    ω→ ∞;  I→ ∞.

3.15.  Компенсация сдвига фаз

Коэффициент мощности (cosφ) приемника с преобладающей индуктивностью L может быть повышен включением батареи конденсаторов параллельно приемнику (рис. 3.37).

Начертим векторную диаграмму, разложим все токи на активные и реактивные составляющие (рис. 3.38).

                     

  Рис. 3.37                                                                                   Рис. 3.38

Из диаграммы имеем:

;         ;

        Ток  выразим двояко:

1)

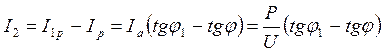
2); приравниваем правые части,

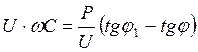, откуда:

                                                 .

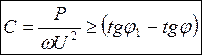Зная С и I2, легко найти реактивную мощность батареи конденсаторов Q, необходимую для заданной компенсации (от φ1 до φ).

,

.      [ВАр], если  Р [Вт]

3.16.   Мгновенная, активная, реактивная и полная мощность цепи переменного тока

Если ток и напряжение в цепи синусоидальны, то их мгновенные значения могут быть записаны так: ; . Здесь угол φ имеет еще свой знак, в зависимости от соотношения xL и xC. Тогда мгновенная мощность цепи будет:

, т.к. , .

С учетом формул тригонометрии   

получаем:

                                     р.                                          (3.52).

Т.о., мгновенная мощность р имеет две составляющие

1) постоянная величина  2) синусоидальная , изменяющаяся с двойной частотой 2ω.

  Средняя мощность за период:

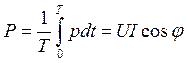, т.к.  интеграл от синусоидальной величины за полный период тождественно равен 0. Средняя мощность , [Вт]  называется также активной.

Рассмотрим частные случаи от общего выражения (3.52) мгновенной мощности.

А. Цепь содержит только активное сопротивление r.

 - намечаем нулевые точки.

;

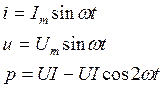
                                                                                              Рис. 3.39

Мощность p всегда положительна, т.е. электрическая энергия идет от                                                   источника к приемнику, полностью   преобразуясь в другие виды (тепло). Средняя мощность  (рис. 3.39).                                             

Б. Цепь содержит только индуктивность L

      Рис. 3.40

1) p>0, когда ток “i” возрастает по абсолютной величине, в этом случае u и iодного знака ( - функция возрастающая. ). Энергия идет от источника и запасается в магнитном поле катушки L (рис. 3.40).

2) p<0, когда ток “i” убывает по оси абсолютной величине, в этом случае u и i разных знаков ( – убывающая функция, ). Магнитное поле катушки L уменьшается до нуля, энергия полностью возвращается источнику. Преобразований ее в другие виды нет. Средняя мощность Р=0.

В. Цепь содержит только емкость С.

Скачать файл