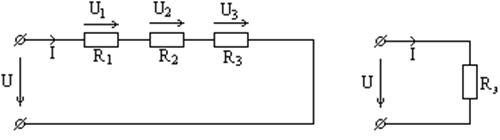
Электротехника \ Электротехника и электроника

, страница 4

Рис. 1.8

По II закону Кирхгофа:

U = U₁+ U₂+ U₃= IR₁+ IR₂+ IR₃= I(R₁+ R₂+ R₃) = IR_Э, (1.21)

где

R_Э=R₁+R₂+R_3. (1.22)

Если сопротивлений не 3 а n, то:

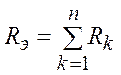, (1.23)

а ток в цепи I=.

1.8 Параллельное соединение сопротивлений

Пусть имеется n параллельно включенных сопротивлений (рис. 1.9):

Рис. 1.9

По I закону Кирхгофа:

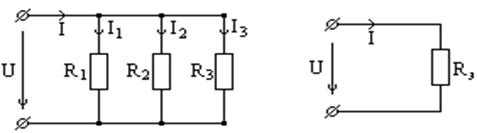
I = I₁+ I₂+ I₃= 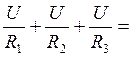U(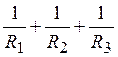). (1.25)

По закону Ома:

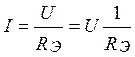. (1.26)

Из сравнения (1.25) и (1.26) имеем:

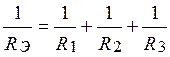, (1.27)

или через проводимость:

q_Э=q₁+q₂+q_3.

Если сопротивление не 3, а n, то:

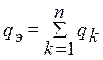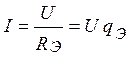, . (1.28)

В частном случае, для 2 сопротивлений полезна формула:

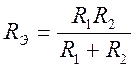. (1.29)

1.9. Смешанное соединение сопротивлений

Это комбинация последовательного и параллельного соединения сопротивлений. Рассмотрим способы расчета смешанного соединения:

1). Вычисление эквивалентного сопротивления.

2). Определение токов по формуле «разброса» Поливанова.

3). Определение токов методом подобия или пропорциональных величин.

1. Рис. 1.10

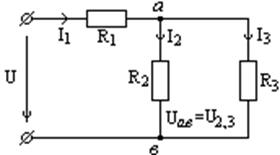R_2,3=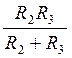; R_Э=R₁+R_2,3;

I₁=; U_2,3= I₁R_2,3= U – I₁R₁;

Рис. 1.10

I₂=, I₃=, I₁= I₁+ I₃ - проверка.

2. Рис. 1.10

R=R₁+,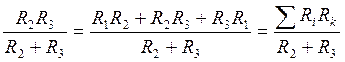

где R_iR_k – сумма попарных произведений из трех сопротивлений.

I=,	U=I×R==,
I=,	В этих формулах в числителе берется «чужое сопротивление».
I=.	В этих формулах в числителе берется «чужое сопротивление».

3. Метод применим только для линейных цепей, т.е. таких в которых R, L, С остаются постоянными и не зависят от величины проходящего через них тока [3].

Для этих цепей при смешанном соединении ток любой ветви пропорционален входному напряжению I_k= a_kU, при этом а_к для каждой ветви имеет свое значение (см. формулы Поливанова).

Метод имеет смысл применять для смешанного соединения с большим количеством ветвей, если требуется определить сразу токи, не вычисляя R, например для следующей схемы (рис. 1.11):

Рис. 1.11

При расчете задаются произвольным током, проще всего 1 А, в ветви, наиболее удаленной от источника

(I¢=1 A).

Затем, используя законы Ома и Кирхгофа, находят токи и напряжения на остальных участках, постепенно приближаясь к источнику. Наконец находят новое значение входного напряжения U¢, вычисляют коэффициент подобия К= и на него умножают все ранее вычисленные токи и напряжения.

2. РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ

Сложной называется такая электрическая цепь, которая не может быть сведена к смешанному соединению сопротивлений. К сложным относятся также цепи, содержащие источники энергии в разных параллельных ветвях.

Примером сложной цепи может быть мостовая схема.

Существует несколько методов расчета сложных цепей, но все они основаны на законах Кирхгофа.

2.1. Непосредственное применение законов Кирхгофа

Пусть дана следующая цепь (рис. 2.1):

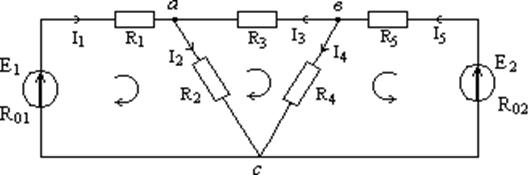
Рис. 2.1

Произвольно намечают стрелками направление токов в ветвях и круговыми стрелками направление обхода независимых контуров.

Число неизвестных токов будет равно числу ветвей. Вначале составляем уравнения по I закону Кирхгофа. Их число равно числу узлов без одного (независимые уравнения).

Остальные уравнения составляются по II закону Кирхгофа с соблюдением знаков (+) и (-) для ЭДС и токов в зависимости от направления обхода контура [4].

С учетом сказанного составляем систему уравнений для заданной схемы:

I₁-I₂+I₃=0,

I₅–I₃–I₄=0,

I₁(R₀₁+ R₁) + I₂R₂= E₁_, (2.1)

I₄R₄– I₂R₂– I₃R₃= 0,

I₅(R₀₂+R₅)+I₄R₄=E₂_.

Решая эту систему, сразу находим токи в ветвях. Если ток получается с (-), то его истинное направление противоположно выбранному.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Скачать файл

Рис. 1.9

По I закону Кирхгофа:

I=,