Расчет электрических цепей: Учебное пособие для студентов, изучающих дисциплины «Электротехника и электроника», «Общая электротехника», «Теоретическая электротехника», страница 17

Если ЭДС симметрична, а сопротивления в отдельных фазах различны, то система токов будет несимметричной.

Таким образом, понятие симметричной трехфазной цепи содержит в себе совокупность симметричной системы ЭДС и симметричной системы токов.

Симметричная система обладает важным свойством:  алгебраическая сумма мгновенных значений ЭДС (напряжений, токов) равна нулю, т.е.

i_а + i_в + i_с  = 0.                                                       (4.3)

Покажем это аналитически:

i_а + i_в + i_с  = Е_м [sinωt+sin(ωt–)+sin(ωt+)] =

= Е_м[sinωt+2sinωtcos(-)] = Е_м(sinωt-sinωt) = 0.

     Тот же результат дает временная и векторная диаграммы.

В комплексной форме это свойство запишется так:

 =0,     =0, 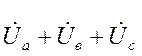    =0.                    (4.4)

4.2.  Соединение источников и приемников электрической энергии звездой и треугольником

Трехфазные цепи могут быть несвязанные и связанные. В несвязанных цепях нет электрических соединений между отдельными фазами. Каждая фаза источника соединяется со своей фазой приемника двумя линейными проводами:  прямым и обратным (на рис. 4.4 – 6 проводов). При связанной системе  (рис. 4.5) отдельные фазы имеют электрические соединения между собой. Например, в рассмотренном случае можно объединить три обратных провода в один, нулевой или нейтральный, ток в котором:

.                                    (4.5)

При симметричной системе =0 и достаточно всего трех линейных проводов

вместо 6 (подключение трехфазных двигателей). Вопросы экономичности заставляют выполнять трехфазные системы связанными.

Существуют два основных способа  связывания трехфазных систем: соединение  звездой и соединение треугольником (есть еще соединение в "зигзаг"). На рис. 4.5 стрелками показано условно положительное направление напряжений и токов.  При соединении звездой все концы обмоток источника (X, Y, Z) соединяются в одной точке 0 – нулевой, или нейтральной точке источника, а начала фаз (А; В; С), соединяются линейными проводами с приемником.

Аналогично, может быть соединен в  и  приемник,  только нулевая точка                     

приемника, объединившая концы его  фаз (х, y, z), теперь называется 0¢. Точки 0 и 0¢ могут соединяться между собой (нулевой или нейтральный провод).

При соединении треугольником конец одной из фаз (например, Х) источника соединяется с началом следующей фазы (например, В) и т.д. до образования замкнутого треугольника. Вершины треугольника соединяются линейными проводами с приемником энергии. На рис. 4.6 стрелками показаны условно положительные направления  напряжений и токов. 

Аналогично, может быть соединен в  Δ  приемник энергии.

Соединение источника и приемника может быть как одинаковым, так и различным. Это зависит от напряжения питающей цепи и номинального напряжения приемника.

ЭДС в фазе источника (т.е. между концом и началом фазы) называется фазной. ().

                    Рис. 4.6

ЭДС между началами разноименных фаз (например, А и В) называется линейной ( или ).

Аналогичное определение можно дать для фазных и линейных напряжений приемника (_ф;  _л   или   ).

Ток в фазе источника или приемника называется фазным  ().

Токи в линейных проводах называются линейными ( или ). Для нулевого и нейтрального провода принят термин – ток в нулевом или нейтральном проводе (I).

4.3.  Соотношения между линейными и фазными величинами

напряжений и токов при соединении звездой

При наличии нулевого провода (рис. 4.7):

По I закону Кирхгофа – ток в нулевом проводе равен геометрической сумме фазных токов:

                                                      .                                                   (4.7)       

Линейные напряжения равны геометрической разности соответствующих фазных напряжений.

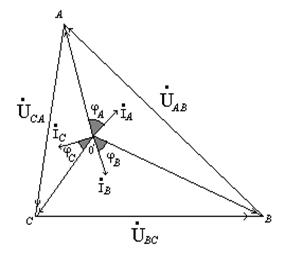В соответствии с уравнением (4.8) построим топографическую векторную диаграмму приемника. Вектора линейных напряжений оказываются направленными противоположно стрелкам этих напряжений на расчетной схеме.