Расчет электрических цепей: Учебное пособие для студентов, изучающих дисциплины «Электротехника и электроника», «Общая электротехника», «Теоретическая электротехника», страница 12

                       Рис. 3.22                                                                              

3.10.  Параллельное  соединение приемников электроэнергии

При параллельном соединении приемников общий ток в неразветвленной части определяется по I закону Кирхгофа как векторная сумма токов отдельных приемников:

  Возьмем для простоты два параллельно соединенных приемника:

              Y₁(q₁,b₁) и Y₂(q₂,b₂) (рис. 3.23).

Тогда:        

                                              .                                                                      (3.49)

По уравнению (3.49) построим для расчетной схемы векторную диаграмму, приняв за исходный вектор напряжение . Затем, на диаграмме, разложим каждый вектор тока на активную и реактивную составляющие (рис. 3.24).

Рис. 3.23

                                                  

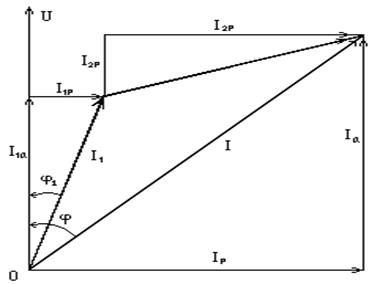
                              Рис. 3.24

Из диаграммы очевидны соотношения:

(1)         - арифметическая сумма;

(2)         - алгебраическая сумма;

       (3)         - векторная сумма.

            Заменив токи произведениями напряжения U на соответствующие проводимости,  по закону Ома имеем:

         

           

        

Здесь:

- арифметическая сумма;                     - алгебраическая сумма, ; - векторная сумма полных проводимостей.

Величину Y можно было бы найти иначе:

.

Произведенный вывод можно распространить на любое число параллельно соединенных приемников, а именно: активные проводимости складывается арифметически; реактивные – алгебраически; полные – как вектора.

Рассмотрим пример в общем виде (3.25), когда заданы полные сопротивления параллельных ветвей, а не их проводимости.

		z1(r1,xL1), z2(r2,xc2).			Последовательность преобразования схем следующая (рис.3.26):
Рис.3.25		I=?     Cosφ=?
а)		q=q+q,                б) в=в+в.

               в)                                                      г)

                                Рис. 3.26

;                             ;                                  ;

; (+)              ; (-)             ;             .

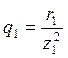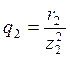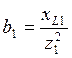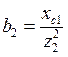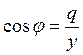3.11.  Смешанное  соединение приемников

 Это соединение рассмотрим на примере в общем виде (рис. 3.27):

Рис. 3.27

Дано: U;  z₁ (r₁, x_L1);

  z₂ (r₂, x_c2);  z₃ (r₃, x_L3).

Найти: I₁; I₂; I₃; U₁; U₂₃=U_ab.

Построить: топографическую векторную диаграмму.

I.          Преобразование схемы.

Вначале найдем величины полных сопротивлений: ;      ;       .
	; ;	.       (-) .      (+)
	; ; .
	; ; .	;      ; .

II. Нахождение величины токов и напряжений:

;          ;           ;      ;      .

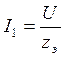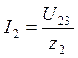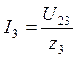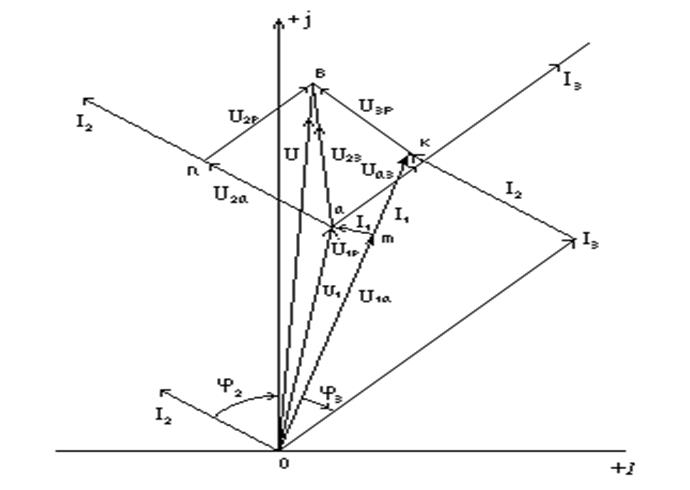
                                        Рис. 3.28

III. Построение топографической векторной диаграммы.

Исходный вектор   (рис. 3.28). Используя треугольники сопротивлений  (r₂; x_c2) и (r₃; x_L3) строим I₂ и I₃. По I закону Кирхгофа строим . Используя (r₁; x_L1) строим напряжение U₁.

По II закону Кирхгофа: 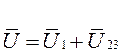. Раскладываем  и  на активные и реактивные составляющие, получаем точки: а, в, m, n, K. Расстояние между ними в масштабе равны соответствующим напряжениям:

                                         

3.12.  Резонанс напряжений

Электрическим резонансом вообще называют такой режим работы пассивнойцепи, содержащей индуктивность L и емкость С, при котором приложенное напряжение U и ток в неразветвленной части цепи I совпадает по фазе, т.е. угол φ=0;

Иными словами, при резонансе электрическая цепь ведет себя как чисто активное сопротивление.

Если в электрической цепи элементы r, L, C соединены последовательно     (рис. 3.29), то возможен резонанс напряжений. Вначале рассмотрим случай идеального резонанса,

т.е. когда катушка L и конденсатор С не содержат                    активного сопротивления. Если по основному условию φ=0, то: