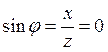Расчет электрических цепей: Учебное пособие для студентов, изучающих дисциплины «Электротехника и электроника», «Общая электротехника», «Теоретическая электротехника», страница 13

. Откуда x=x_L- x_c=0; x_L=x_c или .

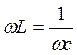        Рис. 3.29

.                                                                           (3.50)

Т.о., резонанса напряжений можно добиться изменением частоты ω, индуктивности L или емкости С, причем можно менять один параметр, два или все три, лишь бы соблюдалось равенство (3.50).

Из (3.50) следует: 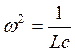; 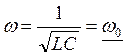, т.е. при идеальном резонансе частота ω равна собственной частоте контура ω_0. Используя это свойство, получим соотношение:

, , При резонансе , значит - минимально, - максимален.

- волновое сопротивление [Ом], - добротность контура, - затухание контура.

Напряжения на элементах контура:

, .  - напряжение цепи. Таким образом, напряжения на L и C равны по величине и противоположны по фазе.

Т.о. напряжения на L и C равны по величине и противоположны по фазе.

При ρ >> r, т.е. при Q >> 1, U_L и U_C могут значительно превосходить U, откуда и происходило название резонанса напряжений. Энергетическое соотношение при резонансе:

; ; ; .

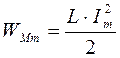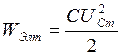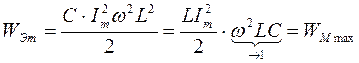При резонансе максимум энергии электрического поля конденсатора равен максимуму энергии магнитного поля катушки индуктивности.

В произвольный момент времени:

; ;

;

.

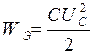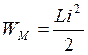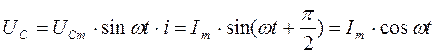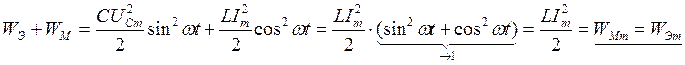Суммарный запас энергии  остается постоянным, равным  или , энергия от источника идет только на покрытие потерь в активном сопротивлении. Приложенное напряжение:

.

Векторная диаграмма при идеальном   резонансе напряжений показана на рис. 3.30.

Для реальной катушки (r,L) и реального конденсатора (r₂, C),  включенных                                 последовательно с реостатом r, векторная диаграмма имеет следующий вид   (рис. 3.31):

          Рис. 3.30                   

; ;

; .

Опасность резонанса напряжений – неучтенное повышение напряжение на отдельных реактивных элементах электрической установки (например, при включении трансформатора (L) на кабель без нагрузки (С)).

        Полезное применение – резонанс широко используется в радиомеханике  для настройки   схем на заданную частоту.

            Рис. 3.31  

3.13.  Резонанс токов

Если в электрической цепи элементы q, L, C соединены параллельно, то возможен резонанс токов (рис. 3.32).В начале рассмотрим случай идеального   резонанса,  т.е. когда катушка L и конденсатор Cне содержат активной

               Рис. 3.32                     проводимости.

 По основному условию резонанса:    φ=0.

Значит, 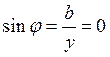; ; , или 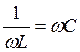, откуда .    (3.51).

Т.о., резонанса токов можно добиться изменением частоты ω, индуктивности L или емкости C, причем можно менять один параметр, два или все три, лишь бы соблюдалось равенство (3.51).

Из (3.51) следует: 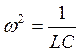; ; 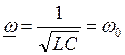т.е. при идеальном резонансе токов частота источника ω равна собственной частоте цепи ω₀. Используя это свойство, получим соотношения:

, . При резонансе , значит проводимость - минимальна, общий ток     ток  - -минимален. Если                           -волновая        проводимость,                           - добротность цепи,                           - затухание цепи.

Тогда токи в отдельных ветвях:

, ,  - общий ток. Т.о. токи в реактивных ветвях L и C равны по величине и противоположны по фазе.

При γ >> q, т.е. при Q >> 1, I_L и I_C могут значительно превосходить I, откуда и происходило название резонанса токов. Энергетические соотношения при резонансе токов:

; ; ; .

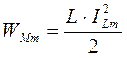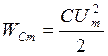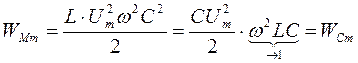При идеальном резонансе токов максимум энергии магнитного поля катушки индуктивности равен максимуму энергии электрического поля конденсатора.

В произвольный момент времени:

; ;

; ;

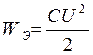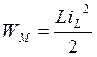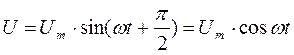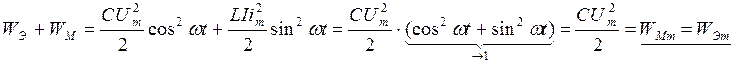
Суммарный запас энергии , энергия от источника идет только на покрытие потерь в активном элементе; катушка и конденсатор обмениваются энергиями.

  Векторная диаграмма при идеальном резонансе токов показана на рис. 3.33.

  Для реальной катушки (q₁, L) идеального конденсатора (q₂, С), включенных параллельно с                               Рис. 3.33                реостатом q, векторная диаграмма имеет вид (рис. 3.34):