Для этого, в отношении выделенной ветви ( ав ) проводят два опыта:
1) холостого хода – замеряют Е![]() = Uавхх вольтметром,
= Uавхх вольтметром,
2) короткого замыкания – замеряют Iкз амперметром.
При коротком замыкании R=0 и по формуле (2.22) имеем:
Iкз = 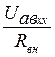 , откуда R
, откуда R![]() =
= 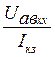 .
(2.23)
.
(2.23)
2.7. Баланс мощности в сложной цепи постоянного тока
Баланс мощности для цепи имеет вид:
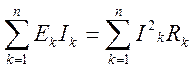 . (2.24)
. (2.24)
При этом надо иметь ввиду правило знаков:
1) в правой части все знаки (+),
2) в левой части равенства будет знак (+), если ЕкÞIк ,
и знак (-), если ЕкÛIк ..
В последнем случае источник перешел в режим работы потребителя энергии. В некоторых случаях уравнение (2.24) легко получить аналитически (рис. 2.11).
|
Рис. 2.11 |
Уравнение первого закона Кирхгофа
I1 –I3 –I2 =0,
умножим на U![]()
I1(E1 – I1R1) – I3(I3R3) – I2(E2 + I2R2) = 0,
тогда:
E1I1 – E2I2 = I12R1 + I22R2 + I32R3.
3. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО ПЕРЕМЕННОГО ТОКА
3.1. Общие сведения
Переменным током вообще называется такой ток, который может изменять как свою величину, так и направление. В начале мы будем изучать периодические переменные токи, значения которых повторяются через равные промежутки времени. Наименьший из таких промежутков называется периодом Т [с].
![]() , (3.1)
, (3.1)
где К – целое число.
Число периодов в секунду называется частотой 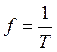 [Гц].
[Гц].
Из периодических функций удобнее для практического
применения такие, среднее значение которых за период равно нулю, т.е. 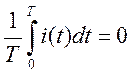 . При этом, самая удобная форма кривой тока
– синусоида.
. При этом, самая удобная форма кривой тока
– синусоида.
Во-первых, синусоида – единственная периодическая функция, имеющая подобные себе по форме производную и интеграл. Действительно, если:
![]() , то
, то ![]() , а
, а 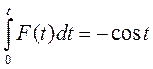 .
.
Это обстоятельство позволяет не искажать форму кривой тока и напряжения при их преобразованиях в различных звеньях электрической цепи. Например:
![]() - обычное умножение
тока,
- обычное умножение
тока,
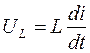 - дифференцирование
тока,
- дифференцирование
тока,
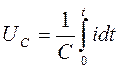 - интегрирование тока.
- интегрирование тока.
Кроме того, значительно, облегчаются расчеты электрических цепей, если токи в них синусоидальны. Можно применить векторные диаграммы и символический метод.
При произвольной форме тока и напряжения функцию разлагают в ряд Фурье, расчет ведут для отдельных гармоник, а затем результаты суммируют по принципу наложения (если цепь линейна). Синусоидальные токи в промышленности получают от машинных генераторов, чаще всего, от трехфазных синхронных генераторов. В основе работы синхронного генератора (рис. 3.1) лежит принцип электромагнитной индукции:
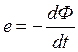 .
.
Свяжем частоту f получаемого тока и напряжения со скоростью ротора генератора “n” и числом пар полюсов “P”. Один оборот соответствует одному периоду.
|
|
Если Р=1, то 1 об/с – 1 Гц,
n об/с – n Гц,
n об/мин – n/60 Гц.
В общем случае, при Р >1
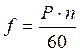 . (3.2)
. (3.2)
Рис. 3.1
В аналитических расчетах чаще пользуются понятием угловой или круговой частоты ω [1/с]:
![]() .
.![]() (3.3)
(3.3)
Аналитическое выражение синусоидального тока и напряжения в одной и той же цепи:
![]() , (3.4)
, (3.4)
![]() ,
(3.5)
,
(3.5)
где:
ί, u – мгновенное значение тока и напряжения;
Im, Um – их максимальные значения (амплитуды);
![]() - фазный угол;
- фазный угол;
ψi, ψu – начальные фазы тока и напряжения, т.е. фазные углы при t=0;
![]() - разность фаз, или
сдвиг по фазе.
- разность фаз, или
сдвиг по фазе.
Знак начальной фазы ψu или ψi определяется по направлению стрелки, проведенной от ближайшего начала синусоиды до начала координат: если стрелка
вправо – (+); влево – (-).
Знак φ на графике определяется направлением стрелки, проведенной от начала синусоиды напряжения до начала ближайшей синусоиды тока.
|
|
В нашем случае на рис. 3.2 ψu (+) ψi (+)
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.