3). Режим короткого замыкания. Напряжение на участке равно нулю (Uкз=0), приемник шунтован очень малым сопротивлением R→0.
4). Согласованный режим – когда пассивный элемент внешней цепи работает с максимальной мощностью при данном источнике.
Легко получить условия согласованного режима. Запишем уравнение электрического состояния простейшей цепи (рис. 1.1):
Е=U+R0I , где U=I·R. (1.17)
R – сопротивление внешней цепи,
R0 – сопротивление источника.
Умножим (1.17) на I :
EI = UI + R0I2,
или
P1=P2+P0,
где
Р1– мощность источника,
Р2– мощность передаваемая во внешнюю цепь,
Р0– мощность потерь внутреннего источника.
Р2=UI= RI2=R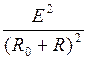
– имеет максимум,
когда величина: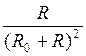
– максимальна т.е.:
,
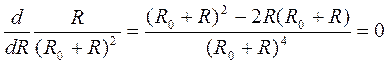или
(R0+R)2–2R(R0+R)=0, R0+R–2R=0, R=R0 .
Следовательно, внешняя цепь и источник работают в согласованном режиме при R=R0 .
Кпд в согласованном режиме равен:
η=
=
=
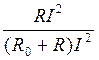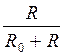=0,5.
С цепями согласованного режима приходится иметь дело тогда, когда низкий кпд не имеет решающего значения из-за малой мощности цепи и когда вопрос максимальной мощности в нагрузке преобладает над соображениями экономического порядка.
1.4 Законы Кирхгофа
А. Первый закон Кирхгофа
Алгебраическая сумма токов в узле электрической цепи равна нулю:
.
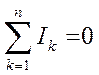(1.18)
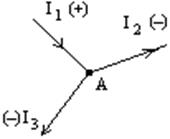I1–I2–I3=0 , или I1=I2+I2 – сумма токов,
входящих в узел равна сумме токов, выходящих из узла (рис. 1.4.).
Первый закон Кирхгофа является частным случаем более общего закона сохранения энергии и выражает тот факт, что ни в одной точке цепи не происходит накопления электрических зарядов.
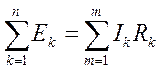. (1.19)
Это тоже частный случай закона сохранения энергии - энергия, выработанная в источниках, полностью потребляется приемниками [2].
1.5 Закон Ома для активного участка цепи
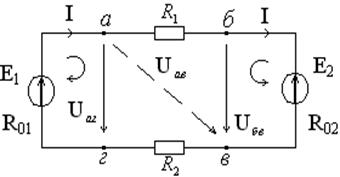
Для определения напряжения Uили тока I на активном участке цепи, т.е. где имеются ЭДС, рассмотрим два возможных случая (рис. 1.5):
.
Любые точки, например аг,
условно замыкаем
Rаг 
,
тогда:
Iаг 
, но
IагRаг = Uаг,, причем
E
> E
.
Рис. 1.5
Случай 1.
По II закону Кирхгофа имеем Е1=IR01 + Uаг; если Uаг известно, то:
I=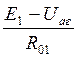 
– генераторный режим.
Случай 2.
Е2 = Uбв – IR02, откуда:
Uбв = Е2 + IR02 , если Uбв известно, то
I=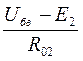 
- двигательный режим.
Уяснив суть закона, запишем Uав через Е1, и через Е2:
Uав = Е1 – I(R01 + R2) = Е2 + I(R02 + R1).
Если Uав известно, то ток I находится:
I=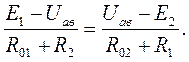 
(1.20)
1.6 Потенциальная диаграмма
Она дает наглядное представление о распределении потенциалов в замкнутой цепи или в контуре сложной цепи.
По оси абсцисс от начала координат (заземленная точка) откладывается в порядке следования сопротивления участков в выбранном масштабе. По оси ординат – потенциалы отдельных точек цепи, которые затем соединяются прямыми линиями. Нулевой потенциал можно дать любой точке. Для построения диаграммы надо знать не условные, а действительные направления токов в ветвях контура, т.е. схема должны быть предварительно рассчитана в числах.
В контуре сложной цепи токи отдельных ветвей могут иметь разное направление, поэтому полезно запомнить следующее правило:
1) при обходе контура по току φ плавно понижается, против тока - плавно повышается;
2) в местах расположения источников происходит скачок φ соответствующего знака.
Рассмотрим сказанное на примере (рис. 1.6 и 1.7):
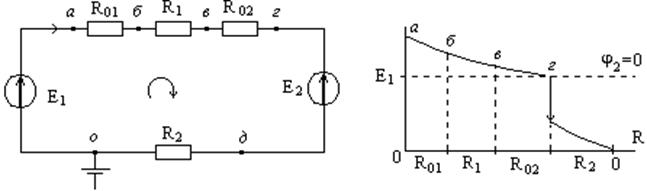
Рис. 1.6 Рис. 1.7
E1 > E2, j0 = 0,
jа = jо + E1 = E1,jг = jв -IR02,
jб = jа -I×R01,jд = jг -E2,
jв = jб -IR1, jо = jд -IR2 = 0 .
1.7 Последовательное соединение сопротивления
Пусть имеется n последовательных соединений сопротивлений (рис. 1.8), входное напряжение цепи U, требуется определить ток в цепи I.
Задача легко решается введением понятия эквивалентного сопротивления RЭ. При эквивалентной замене группы сопротивлений одним или другой группой токи и напряжение в остальной части цепи, не подвергающейся преобразованию, остаются без изменения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.