|
|
Учитывая сказанное, мгновенные значения i и u в одной и той же цепи, надо записывать в следующем виде:
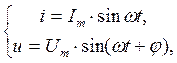 , или
, или 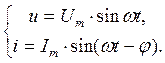 (3.40)
(3.40)
В этих равенствах для φ имеет место знак:
(+)
– если ![]() ,
,
(–)
– если ![]() .
.
3.8. Активная, реактивная, полная проводимости
|
|
При расчете последовательного соединения (r, x) общее напряжение цепи Uчасто раскладывается на активную и реактивную составляющие (рис. 3.17):
![]() .
(3.41)
.
(3.41)
В параллельных цепях удобнее раскладывать на составляющие ток в неразветвленной части (рис. 3.18). Непосредственно из векторной диаграммы следуют отношения:
Рис 3.17
|
|
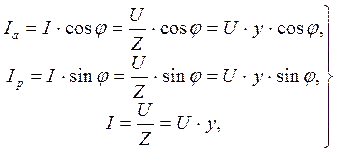 (3.42)
(3.42)
Рис. 3.18 где Z – полное
сопротивление цепи, а 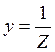 -
полная проводимость цепи.
-
полная проводимость цепи.
Введем
следующие понятия и обозначения: ![]() - активная проводимость
цепи,
- активная проводимость
цепи, ![]() - реактивная проводимость цепи (рис. 3.19).
Тогда соотношение (3.42) запишется так:
- реактивная проводимость цепи (рис. 3.19).
Тогда соотношение (3.42) запишется так:
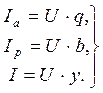 (3.43)
(3.43)
Используя (3.43), поделим все стороны треугольника токов MONна величину напряжения U и получим подобный ему треугольник (рис. 3.19) проводимостей:
|
|
Из
него очевидны соотношения, позволяющие определить угол φ: 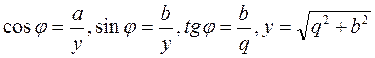 . (3.44)
. (3.44)
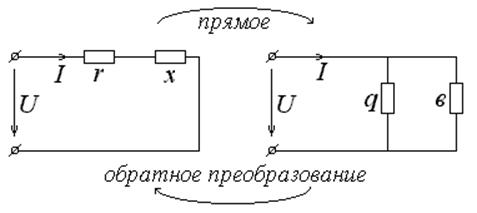
Используя треугольник сопротивлений и треугольник проводимостей, выведем формулы прямого преобразования, позволяющее заменять последовательное соединение (r,x) эквивалентным параллельным (q,b):
Рис. 3.19
|
|
Откуда:
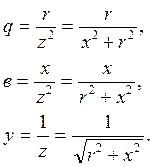 (3.45)
(3.45)
В частном случае:
1) r = 0; q = 0; b = 1/x; y = 1/ x= b.
2) x = 0; b = 0; q= 1/r; y=1/r=q.
Формулы обратного преобразования, позволяющие заменять параллельное соединение (q, b) эквивалентно последовательным (r, x) (рис. 3.20) получим непосредственно из формул (3.45):
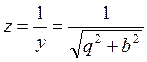 ,
,
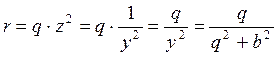 ,
(3.46)
,
(3.46)
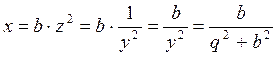 .
.
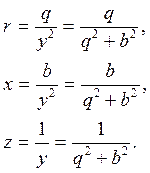 (3.47)
(3.47)
В частном случае:
1) q = 0; r = 0; x = 1/b; z = 1/b = x.
2)b=0; x= 0; r= 1/q; z= 1/q= r.
3.9. Последовательное соединение приемников электроэнергии
При последовательном соединении приемников электроэнергии общее напряжение цепи определяется по II закону Кирхгофа как векторная сумма напряжений отдельных приемников:
![]()
![]() (3.48)
(3.48)
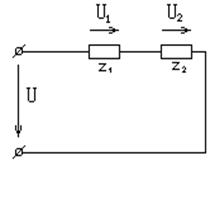
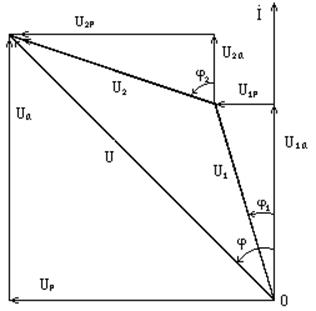
Возьмем два последовательно соединенных приемника z1(r1,x1) и z2(r2,x2) (рис. 3.21). . По уравнению (3.48) построим для данной схемы векторную диаграмму (рис. 3.22), приняв за исходный вектор тока I. Затем по диаграмме разложим каждый вектор напряжения на активную и реактивную составляющие.
Рис. 3.21
Из диаграммы очевидны соотношения:
(1) ![]() - арифметическая сумма;
- арифметическая сумма;
(2) ![]() - алгебраическая сумма;
- алгебраическая сумма;
(3) ![]() - векторная сумма.
- векторная сумма.
Заменим напряжения произведениями тока на соответствующие сопротивления по закону Ома:
|
|
|
Величину z можно было бы найти иначе:
![]() .
.
Произведенный вывод можно распространить на любое число последовательно соединенных приемников, а именно: активное сопротивление складывается арифметически; реактивное – алгебраически; полное – как вектора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.