Расчет электрических цепей: Учебное пособие для студентов, изучающих дисциплины «Электротехника и электроника», «Общая электротехника», «Теоретическая электротехника», страница 6

Рис. 2.4

I1 = I¢1 – I¢1, I2 = I¢¢2 – I¢2, I3 = I¢¢3 + I¢3.

При числовом решении действующий ток в ветви получает направление большего тока.

 

Метод применим лишь для определения токов и напряжений, но не применим для квадратичных форм от тока (мощности, энергии, пропорциональных I²).

Метод неудобен: когда много источников, когда частичная схема  не смешанное соединение, а сложная цепь; когда частичные токи одной ветви мало отличаются друг от друга по величине, а надо брать их разность (возможна большая ошибка).

2.5.  Преобразование треугольника сопротивлений в эквивалентную звезду и обратно

Такое преобразование часто позволяет свести сложную цепь к смешанному соединению, что сразу упрощает расчет. Пример – мостовое соединение сопротивлений (рис. 2.5 и 2.6).

Рис. 2.5                                                                                  Рис. 2.6

По законам Кирхгофа - система из 6 уравнений.

Обычное смешанное соединение.

Формулы преобразования будут выведены из условия эквивалентной замены D на  (рис. 2.7):

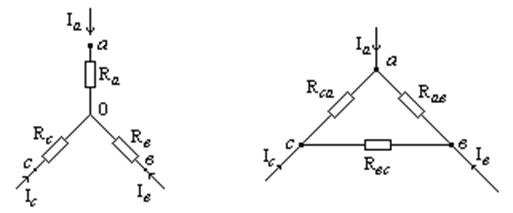
Рис. 2.7

I_c = 0;  a®в: R_a + R_в =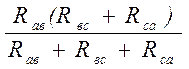,                       (2.5)

I_a = 0;  в ®с : R_в + R_c =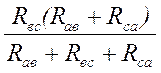,                  (2.6)

I_в = 0;  с ®а : R_c + R_a = 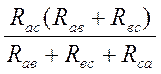.                             (2.7)

Из (2.5) вычтем (2.6):   R_a  – R_c = 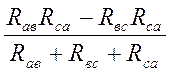,                                  (2.8)

и прибавим (2.7):         R_a + R_c = 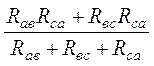.                                                (2.9)

Подмечая закономерность, напишем сразу все 3 формулы преобразования

R_a = 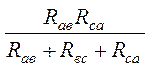,                                             (2.10)

R_в = 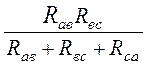,                                             (2.11)

R_c = 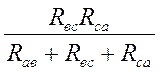.                                            (2.12)

В частном случае, если  R_ав = R_вс = R_са = RD то:                                                                                  R=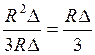,      R=.                                                      (2.13)

Формулы обратного преобразования, т.е. из  в D, можно получить, если перемножить почленно и попарно равенства (2.10), (2.11), (2.12) и их сложить:

R_аR_в + R_вR_с + R_сR_а = 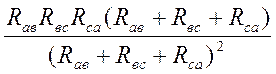,                              (2.14)

R_аR_в + R_вR_с + R_сR_а = 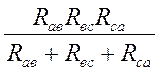,                                       (2.15)

R_с = 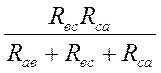,                                                            (2.16)

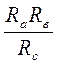 + R_в + R_а = R_ав.                                                                (2.17)

Подмечая мнемоническую закономерность, напишем сразу 3 формулы обратного преобразования:

R_ав = R_а + R_в + 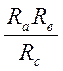,                                          (2.18)

R_вс = R_в + R_с + 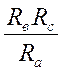,                                           (2.19)

R_са = R_с + R_а + 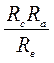.                                           (2.20)

В частном случае, если R_а=R_в=R_с=, то R_D=++.

R_D=3.

2.6.  Метод эквивалентного генератора

В некоторых случаях необходимо исследовать режим работы только одной ветви сложной цепи при изменении сопротивления этой ветви; в остальных ветвях цепи ЭДС и сопротивления остаются неизмененными.

При таких условиях, вместо повторных  громоздких расчетов, целесообразно воспользоваться методом эквивалентного генератора.

Поэтому выделяют нужную ветвь, а всю остальную часть схемы представляют активным двухполюсником. Этот двухполюсник рассматривают как эквивалентный генератор (рис. 2.8).

Рис. 2.8

Для расчета надо знать ЭДС. Е генератора и его внутреннее сопротивление R_вн . ЭДС Е принимают равной напряжению схемы на зажимах разомкнутой исследуемой ветви ( ав ).

Е=U.                                     (2.21)

R_вн - генератора подсчитывают как R_вхав при закороченных источниках питания, а их внутренние сопротивления остаются.

Тогда расчетная схема приобретает вид, показанный на рис. 2.9.

Рис. 2.9

Из 2-го закона Кирхгофа для схемы (рис. 2.9) имеем:

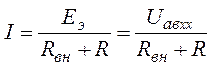.                                      (2.22)

Меняя R в исследуемой ветви, можно составить таблицу и по ней построить график  I= f(R) (рис. 2.10).

Рис. 2.10

Имея график (рис. 2.10), можно сразу найти ток Iпри любом изменении R.

На практике очень важно, что Е и R_вн  генератора могут быть определены опытным путем.