|
|
1) p>0,
когда напряжение “u” возрастает по абсолютной величине, в этом случае u
и iодного
знака ( 2) p<0, когда “u” убывает
по абсолютной величине (We – убывающая функция, |
Г. Цепь содержит r и x.
|
Рис. 3.42 |
Большую часть периода Т p > 0, т.е. энергия идет от источника к приемнику, преобразуясь в другие виды (например, в тепло) и частично запасается в полях приемника. (u и i одного знака). Меньшую часть периода Т p <0,
энергия полей приемника возвращается источнику (u и i
разных знаков) Средняя мощность Тогда активная мощность |
P, Qи Sсвязаны между собой теоремой Пифагора:
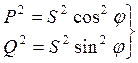 ,
, ![]() . Откуда:
. Откуда: ![]() .
.
Эта связь позволяет построить следующий треугольник мощностей (рис. 3.43).
|
|
Из него можно найти угол φ:
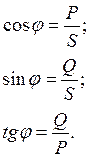
Рис. 3.43
3.17. Символический или комплексный метод расчета цепей переменного тока
Этот метод расчета применим к цепям синусоидального тока и позволяет геометрические операции над векторами электрических величин (e, u, i), заменить алгебраическими операциями над соответствующими комплексными числами. Метод основан на том, что любой вектор на плоскости можно изобразить комплексным числом.
Для этого выбирают комплексную плоскость, в которой лежит данный вектор, и проводят в этой плоскости под прямым углом друг к другу две оси: горизонтальную – вещественную и вертикальную – мнимую.
Вектор переносят параллельно самому себе началом в начало координат и проектируют на оси, тогда проекции вектора будут соответствовать вещественной и мнимой части комплексного числа, записанного для конца вектора (рис. 3.44),
|
Рис. 3.44 |
причем:
![]() - мнимая единица.
- мнимая единица.
Комплексное число может быть записано в трех формах: алгебраической, тригонометрической и показательной:
![]() . Здесь использованы следующие
формулы перехода:
. Здесь использованы следующие
формулы перехода:
|
|
|
Для сложения и вычитания удобнее алгебраическая форма, для остальных действий – показательная.
Пусть имеется два комплексных числа:
![]() и
и ![]() .
.
|
|
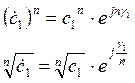 . .
|
Рассмотрим умножение комплексного числа на
единичный комплекс ![]() :
:
![]() .
.
В результате умножения модуль числа ċ не
изменяется, а аргумент увеличивается на величину ![]() .
.
Пусть 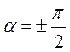 , тогда
, тогда 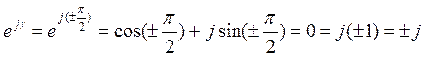 .
.
Таким
образом, умножение вектора на ±jсоответствует его повороту на угол ![]() .
.
Неподвижные вектора электрических величин ![]() записываются в комплексной форме как
обычные вектора.
записываются в комплексной форме как
обычные вектора.
Если же нужно записать комплексным числом мгновенное значение электрических величин i, u, e, то нужно аргумент комплексного числа γ сделать зависящим от времени:
![]() .
.
Рассмотрим следующее комплексное число с переменной γ
![]() . (3.53)
. (3.53)
Теперь сравним с ним мгновенное значение тока (две формы записи):
![]() - мнимая часть исходного
комплексного числа,
- мнимая часть исходного
комплексного числа,
![]() - реальная часть исходного комплексного числа.
- реальная часть исходного комплексного числа.
Запишем равенство (3.53) в другом виде:
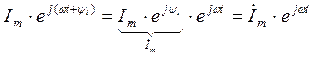 ,
,
где ![]() - комплексная амплитуда, а
- комплексная амплитуда, а ![]() - оператор поворота.
- оператор поворота.
Разделив
предыдущее равенство на ![]() , получим:
, получим:
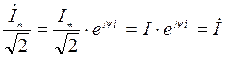 - комплекс действующего
значения тока.
- комплекс действующего
значения тока.
1. Закон Ома
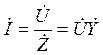 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.