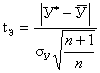Методические указания к практическим занятиям по дисциплине "Основы научных исследований", страница 9

.                                                        (3.13)

Полученное значение  сравнивают с табличным  (таблица 1 Приложения) при заданной (принятой) надежности вывода Р. Если при данном числе n измерений и принятой надежности Р окажется, что  > , то «выскакивающее» значение  содержит грубую ошибку и его следует исключить из дальнейшей обработки результатов.

При неизвестной   вместе неё применяют , вычисленную по равенству (5.4), а значение  определяют из соотношения

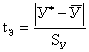.                                                          (3.14)

5.4. Сравнение двух средних значений

Иногда в процессе эксперимента появляется необходимость выявления причины различия между   и , полученных в разных сериях измерений, возможно выполненных в разное время, но при одних и тех же условиях эксперимента и одними и теми же приборами. Однако обнаружено, что  и  отличаются друг от друга. Возникает подозрение – это отличие вызвано случайными ошибками эксперимента или неслучайными.

Измерения в каждой серии предполагаются независимыми и равноточными, а распределение ошибок измерений – нормальным.

При известных величинах  и  по выражению

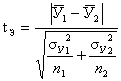,                                                          (3.15)

где n₁ и n₂  – количество повторных измерений в первой и второй серии, соответственно, определяется экспериментальное значение t– критерия, которое сравнивается с его табличным значением при принятой вероятности Р вывода. Если t_Э < t_ТАБ, то расхождение  и  можно считать случайным с надежностью Р. В противном случае расхождение неслучайно, а вызвано определенными причинами, которые необходимо установить.

При неизвестных также принимается гипотеза о равноточности измерений в обоих сериях, а подсчитывается по выражению

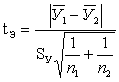,                                                        (3.16)

где 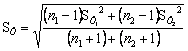                          ,                                                             (3.17)

а                                   ,        .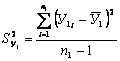

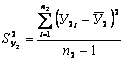Далее по желаемой Р находится табличное значение  – критерия, т.е. t_ТАБ=t(P,n₁+n₂-2), которое сравнивается с t_Эпо условию t_Э<t_ТАБ.

3.5. Сравнение дисперсий

Для оценки равноточности или однородности выполненных измерений в разных сериях повторных опытов часто требуется сделать сравнение их дисперсий.