В
матрице приведены кодированные значения уровней факторов – (+1) и (-1), где, соответственно,
+1 ≡ ![]() , а –1 ≡
, а –1 ≡ ![]() ,
,
 ,
(5.1)
,
(5.1)
гдеХi– кодированное значение i–го фактора,
![]() –
натуральное значение i–го фактора,
–
натуральное значение i–го фактора,
![]() –
нулевое (среднее) значение i–го фактора между его максимальным и минимальным
натуральным значением, т.е.
–
нулевое (среднее) значение i–го фактора между его максимальным и минимальным
натуральным значением, т.е.
![]() ,
(5.2.)
,
(5.2.)
![]() – интервал варьирования i–го
фактора от его среднего (нулевого) значения до максимального или минимального
натурального значения.
– интервал варьирования i–го
фактора от его среднего (нулевого) значения до максимального или минимального
натурального значения.
После составления матрицы ПФЭ–2К разрабатывается план эксперимента, в котором для каждого опыта (строки плана) значения факторов прописывают в натуральном виде. Последовательность опытов рандомизируют с помощью таблицы случайных чисел или лотереи.
После реализации плана эксперимента, т.е. заполнения графы У, с учетом повторов каждого опыта n раз, приступают к статистической отработки результатов ПФЭ – 2К в следующей последовательности:
1. Исключают «промахи», т.е. грубые результаты в сериях повторных опытов для каждой строки плана.
2. Вычисляют среднее значение параметра У исследуемого объекта по строкам плана
![]() . (5.3)
. (5.3)
3. Вычисляют построчные дисперсии
![]() .
(5.4)
.
(5.4)
4.
Проверяют гипотезу однородности построчных дисперсий ![]() .
.
5.
Вычисляют дисперсию воспроизводимости ![]() для
всего эксперимента
для
всего эксперимента
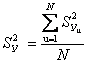 .
(5.5)
.
(5.5)
6. Вычисляют все коэффициенты идентификационной регрессионной математической модели параметра У в виде
![]() (5.6)
(5.6)
по следующим
формулам: 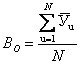 ,
(5.7)
,
(5.7)
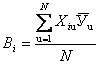 , (5.8)
, (5.8)
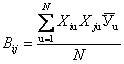 ,
(5.9)
,
(5.9)
где ![]() – кодированные значения уровней i–го
j–го факторов в u -ом опыте матрицы плана,
– кодированные значения уровней i–го
j–го факторов в u -ом опыте матрицы плана,
![]() – среднее значение параметра У
исследуемого объекта в u -ом опыте матрицы плана.
– среднее значение параметра У
исследуемого объекта в u -ом опыте матрицы плана.
7.
Вычисляют дисперсию коэффициентов математической модели ![]()
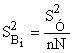 ,
(5.9)
,
(5.9)
и их ошибку
![]() ,
(5.10)
,
(5.10)
а также доверительный интервал
![]() ,
(5.11)
,
(5.11)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.