Методические указания к практическим занятиям по дисциплине "Основы научных исследований", страница 8

         σ_У = ℓim S_У                                                             (3.6)

n→∞

Вероятность (надежность) Р того, что из n измерений Р∙n измерений не будут выходить за пределы , а  (1-Р)∙n измерений будут выходить за эти пределы называется доверительной вероятностью, а интервал  – доверительным интервалом.

Расчет  зависит от закона распределения У в n измерениях. При n ≥15 принимают нормальный закон распределения,  – как математическое ожидание среднего,      и     .                                                    (3.7)

При n ≤15 принимается распределение Стьюдента и

,                                             (3.8)

где       и    – критерий доверительной вероятности Р или критерий Стьюдента.

По правилу 3 σ (трех сигм) ошибка всегда меньше чем

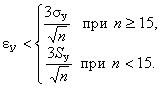                                                 (3.9)

Оценка точности непрямых измерений параметра У являющегося функцией других факторов  и по которым имеются данные измерений, осуществляется по формуле:

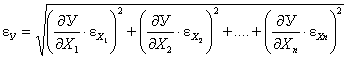,                         (3.10)

где     ,  , ….,   – ошибки измерений факторов.

3.2. Расчет необходимого количества измерений в одном и том же опыте

Необходимое количество измерений величины У с доверительной оценкой и надежностью  Р можно определить заранее, если известна воспроизводимость измерений и все n измерений равноточны. В этом случае из равенства (3.7) находим

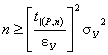.                                           (3.11)

Если  неизвестна, то необходимо сделать 3-4 измерения, оценить по ним  и на базе равенства (3.8) определить

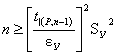.                                           (3.12)

Аналогичную процедуру определения можно выполнить, пользуясь правилом 3 σ (3.9).

3.3. Исключение грубых ошибок

Браковка «выскакивающего» (грубого) значения некоторого из параллельных (повторных) опытов осуществляется путем сравнения его с остальными данными измерений.

При известной  (истинное значение средне квадратичной ошибки) подсчитывается  среднее арифметическое ряда повторных измерений , ,…,  без ,в котором подозревается грубая ошибка. Затем абсолютную разность

 сравнивают с величиной  путем определения экспериментального значения критерия Стьюдента