Методические указания к практическим занятиям по дисциплине "Основы научных исследований", страница 12

–  логарифмическая – ;

–  гиперболическая – У=В₁/Х и др.

Для определения параметров (коэффициентов) регрессионных моделей применяют:

–  метод выбранных точек;

–  метод средних;

–  метод наименьших квадратов (МНК).

Наиболее точным и надежным методом определения коэффициентов (В_О, В₁ , В2, …) регрессионной модели является МНК, т.к. он предусматривает выполнение условия

,                                           (4.1)

где  – фактическое (экспериментальное, наблюдаемое) значение показателя У;

        – значение показателя У, вычисленное по регрессионной модели.

Тесноту связи между У и Х определяет коэффициент корреляции

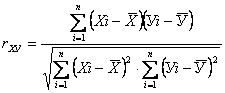.                                    (4.2)

При  между У и Х отсутствует корреляционная связь, а при – связь высокая. Если же , то имеем функциональную связь.

Оценка статической значимости коэффициентов регрессии осуществляется с помощью t– критерия. Расчетное значение t – критерия определяется для каждого коэффициента по формуле:

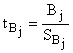,                                                    (4.3)

где     – среднее квадратичное отклонение для  , равное для .

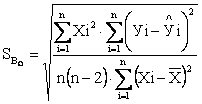,                                     (4.4)

а для остальных коэффициентов

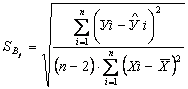.                                              (4.5)

Критическое значение t – критерия определяется по таблице t – распределения (таблица 1 Приложения), задаваясь уровнем значимости Р и  n –1 степенями свободы. Затем сравнивают t_ТАБ  с  t_Во  и t_Вj.

И если   t_Во, t_Вj  > t_ТАБ, то коэффициенты Во, В₁ В₂ , …    статистически значимы с заданным уровнем надежности Р.

Проверка на адекватность регрессионной модели осуществляется по критерию Фишера, расчетное значение которого равно

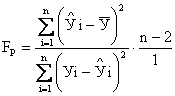.                                         (4.6)

Критическое значение F – критерия определяется по таблице F – распределения (таблица 2 Приложения), задаваясь уровнем значимости Р и  n – 2 степенями свободы.

Сравнивая F_ТАБ и F_Р по условию       F_ТАБ<F_Р                                           (4.7)    

устанавливают адекватность построенной регрессионной модели с надежностью Р.

Расчетное значение F – критерия для многофакторной регрессионной модели определяют по выражению

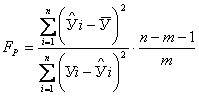,                                (4.8)

где     m  – число факторов.

Расчет средне квадратичного отклонения для коэффициентов многофакторной регрессии выполняют по формулам:

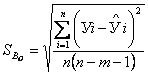,                 (4.9) 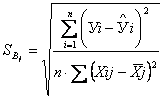     .         (4.10)