Методические указания к практическим занятиям по дисциплине "Основы научных исследований", страница 17

где   – критерий Стьюдента с принятым уровнем значимости Р.

8.  Проверяют статистическую значимость всех вычисленных коэффициентов математической модели по условию

                                                  (5.12)

9.  Математическую модель параметра после исключения незначимых членов проверяют на адекватность с помощью F – критерия, для чего вычисляют его расчетное значение

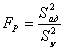   ,                                                 (5.13)

где                                      ,                                                 (5.14)

       – значение параметра У вычисление по математической модели;

       L – число коэффициентов, входящих в математическую модель после исключения незначимых.

Табличное значение F – критерия находится при задаваемой надежности Р, K₁ = N–L, K₂ = (n – 1)N.

Если  F_Р < F_ТАБ,                                                                                                      (5.15)

то построенная по результатам эксперимента математическая модель параметра У адекватно описывает его зависимость от факторов Х₁, Х₂,….., Х_К.

Вывод об адекватности математической модели можно сделать и без проверки по условию F_Р < F_ТАБ,  если 

.                                                    (5.16)

5.4. Дробный факторный эксперимент 1-го порядка

При увеличении числа факторов план ПФЭ – 2^К становится громоздким, т.к. число опытов (строк плана) возрастает пропорционально степени 2^К. Например, при К = 5, N =32 ,а при К = 8 число опытов уже равно N = 256 и т.д. Такие планы позволяют построить математические модели с 2^К членами. Но в таких моделях эффекты взаимодействий 3-х, 4-х и более факторов часто статистически не значимы. Учитывая это, можно в столбцы таких незначимых взаимодействий матрицы плана ПФЭ – 2^К ввести новые факторы и тогда получим матрицу дробного факторного эксперимента типа ДФЭ – 2^К-Р, где Р – число линейных эффектов приравненных к эффектам взаимодействий. Например, в плане 2² эффект взаимодействия Х₁, Х₂  можно приравнять новому фактору Х₃ и тогда N = 2^3-1 =4, вместо N³=8. Также в плане 2³ эффект взаимодействия   Х₁ Х₂ Х₃ = Х₄,  а Х₁Х₃ = Х₅ и тогда N = 2^5-2 = 8, вместо N⁵=32.

Статистическая обработка планов ДФЭ – 2^К-Р проводится также как и планов ПФЭ – 2^К.

5.5. Факторные планы 2-го порядка

Планы 2-го порядка позволяют получить квадратичную полиномиальную модель вида

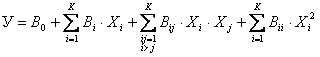,               (5.17)

которая учитывает не только линейные эффекты факторов и эффекты их взаимодействия (как в модели 1-го порядка), но и квадратичные эффекты каждого фактора. Например, для двухфакторного процесса У(Х₁,Х₂) имеем

.

Для получения таких моделей уже необходимо варьирование факторов не менее чем на 3-х уровнях.