Методические указания к практическим занятиям по дисциплине "Основы научных исследований", страница 21

Тема 6. Планирование экспериментов в задачах  оптимизации или поиска экстремальных условий

Необходимость в решении оптимизационных задач часто возникает при проведении научных исследований.

Большое значение имеет оптимизация производственных процессов и режимов эксплуатации технических объектов.

Поиск оптимальных условий исследуемого процесса особенно осложняется при наличии большого числа влияющих факторов, а также при наличии  нескольких выходных параметров (критериев оптимальности). Оптимизация процесса представляет собой целенаправленный поиск значений влияющих факторов, при которых достигается экстремум его (процесса) критерия оптимальности.

Известно достаточно большое число методов поиска оптимума исследуемого многофакторного процесса. Наиболее известными и широко используемыми являются метод крутого восхождения (спуска) и последовательный симплексный метод поиска оптимума.

6.1. Метод крутого восхождения

Для метода крутого восхождения (спуска) или метода Бокса–Уилсона при поиске области оптимума использовано свойство градиента (антиградиента) – направление кратчайшего пути к области экстремума.

Известно, что градиентом многофакторной функции называют вектор

,

где – орты осей факторного пространства.

Область оптимума можно найти путем движения по градиенту линейного приближения многофакторной функции, которой может быть регрессионная модель типа  (7.6). Коэффициенты такой модели являются оценками частных производных функции параметра (критерия) оптимизации  , т.е.             .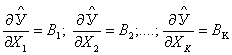

Изменяя  факторы (независимые переменные) пропорционально величинам коэффициентов регрессии, можно двигаться в направлении градиента параметра оптимизации по самому крутому пути.  Именно поэтому процедура движения к оптимуму по градиенту называется крутым восхождением (спуском).

В многофакторном пространстве движение начинают из центра плана ().

Координаты новой точки в направлении градиента получают путем прибавления величины

, называемой шагом движения, т.е.:

,   ,   ….. ,

.

Вспомогательный множитель  определяет длину и направление шага движения по градиенту или антиградиенту.

Процедура метода шагового движения по градиенту (антиградиенту) следующая.

Один из значимых факторов модели принимают за базовый.  Для него вычисляют произведение ,

где  – коэффициент линейной математической модели (при кодированных значениях факторов) при факторе ,     

 – интервал варьирования фактора .

Для базового фактора выбирают шаг движения , исходя из условия,  принимая, как правило, .

Находят величину вспомогательного множителя : .

Затем рассчитывают шаги движения по остальным факторам по формуле:

.