Методические указания к практическим занятиям по дисциплине "Основы научных исследований", страница 10

1. Сравнение двух дисперсий. Для решения вопроса о случайном или неслучайном расхождении двух дисперсий необходимо определить величину отклонения большей дисперсии к меньшей :

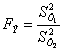,                                                     (3.18)

которую называют экспериментальным значением критерия Фишера.

Затем задавая желаемую надежность вывода Р по таблице F – критерия определяют табличное значение критерия Фишера F_ТАБ  (таблица 2 Приложения), которое сравнивают с F_Э .

Если  F_ТАБ > F_Э , то расхождение дисперсий можно считать незначительным, т.е. данные измерений равноточны с надежностью Р, в противном случае таких оснований не имеется. При этом .

2. Сравнение ряда дисперсий. Если имеем несколько серий повторных измерений при одинаковой численности повторов в каждой серии в одном и том же эксперименте с отличающимися дисперсиями, то для оценки их однородности, т.е. одинаковости их разброса относительно средней, вычисляют экспериментальное значение критерия Кохрена по выражению:

,                                        (3.19)

где  – дисперсия с максимальным значением  из ряда сравниваемых дисперсий.

Затем находится табличное значение G – критерия (таблица 3 Приложения), как  и сравнивается с G_Э. Если G_ТАБ > G_Э, то все дисперсии однородны с надежностью Р. В противном случае гипотеза об однородности сравниваемого ряда дисперсий не подтверждается.

3.6. Практическое задание по теме 3

Выполнить решение следующих задач по оценке точности данных измерений:

Задача 1. Для ряда повторных измерений (10, 18, 15, 20, 19, 14, 15, 12, 13, 18) определить среднее арифметическое, дисперсию и среднее квадратичное отклонение.

Задача 2. По исходным данным задачи 1 определить возможность наличия грубой ошибки в измерениях с цифрами «10» и «20».

Задача 3. Выполнено 10 измерений вертикального раскрытия трала h_Т и = 46,1 м. Определить доверительный интервал для h_Т при доверительной вероятности Р = 0,95.

Задача 4. По исходным данным задачи 3 определить отклонения истинного значения измеренного значения h_Т от его среднего арифметического , исходя из правила 3 σ.

Задача 5. Две серии равноточных измерений нагрузки в ваерах трала  235,6 кН и  228,0 кН., выполненные в разные дни, при n₁= 25 и n₂ = 50 . Определить значимость расхождения средних арифметических  и .

Задача 6.  Для шести повторных серий опытов получено = 3,82, = 1,70, = 1,30, = 0,92,  = 0,78, = 0,81. Определить однородность полученного ряда дисперсий при Р = 0,95.