Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 9

          Рассмотрим решение задачи оценки устойчивости и качества переходных процессов СУ с помощью метода логарифмических характеристик. Для решения задачи необходимо по заданной ПФ СУ построить ЛХ. В качестве примера воспользуемся ПФ астатической СУ 2 (1.5): 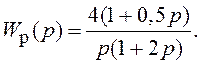 СУ содержит следующие типовые элементарные звенья: усилительное, интегрирующее, апериодическое и форсирующее. Коэффициент усиления переводим в дБ: 4→20lg4=20lg2²≈2∙6=12 дБ. Определяем частоты сопряжения апериодического (ω_с1=0,5) и форсирующего (ω_с2=2) звеньев. При построении ЛАХ можно формально изобразить ЛАХ перечисленных типовых элементарных звеньев и выполнить их графическое суммирование. Однако существует более удобный способ построения ЛАХ. Сначала строится низкочастотная асимптота ЛАХ с учетом следующих соображений: низкочастотные асимптоты ЛАХ апериодического и форсирующего звеньев представляют собой горизонтальные прямые на уровне 0 дБ и, следовательно, не влияют на построение низкочастотной асимптоты итоговой ЛАХ системы. Поэтому из W_р(jω) убираем ПФ апериодического и форсирующего звеньев и для оставшейся ПФ строим низкочастотную асимптоту. Для этого через точку на оси ординат, соответствующую коэффициенту усиления системы (в нашем примере 12 дБ), проводится прямая с наклоном -6r дБ/окт., где r – количество интегрирующих звеньев в W_р(jω) (в нашем примере r=1). Это и есть низкочастотная асимптота нашей ЛАХ. Далее, двигаясь вдоль оси абсцисс слева направо, изменяем наклон ЛАХ по мере включения апериодического и форсирующего звеньев. При включении апериодического звена наклон ЛАХ увеличивается (добавляется -6 дБ/окт., начиная с его частоты сопряжения), а при включении форсирующего звена наклон ЛАХ уменьшается (добавляется +6 дБ/окт., начиная с его частоты сопряжения).

          В нашем примере W_р(jω) содержит 1 интегратор (r=1), следовательно, низкочастотная асимптота ЛАХ имеет наклон -6 дБ/окт. и проходит через точку 12 дБ на оси ординат (рис. 1.25). С ростом частоты первым включается аперио-

дическое звено, следовательно, начиная с частоты ω=ω_с1 наклон ЛАХ увеличивается до -12 дБ/окт. (это среднечастотная асимптота нашей ЛАХ). Далее на частоте ω=ω_с2 включается форсирующее звено и наклон ЛАХ уменьшается до -6 дБ/окт. (это высокочастотная асимптота нашей ЛАХ). При построении ЛФХ следует формально изобразить ЛФХ перечисленных типовых элементарных звеньев и выполнить их графическое суммирование.

          Характерными точками ЛХ являются: коэффициент усиления K (точка пересечения низкочастотной асимптоты и оси ординат), частота среза ω_ср (точка пересечения ЛАХ и оси абсцисс), запас устойчивости по фазе .

          При определении показателей качества СУ прежде всего интересуются устойчивостью. Для этого следует убедиться в наличии запаса устойчивости по фазе: γ>0 (если , то система неустойчива). В нашем примере , следовательно, система устойчива.

          Для оценки качества переходных процессов определяются вспомогательные характеристики: степень колебательности, величина перерегулирования и время нарастания переходного процесса.

          При использовании метода ЛХ в зависимости от степени колебательности различают монотонные (апериодические) или близкие к ним переходные процессы, слабоколебательные переходные процессы и сильноколебательные переходные процессы. Классификация переходных процессов выполняется в зависимости от величины запаса устойчивости по фазе γ (рис. 1.26):

  - монотонный (апериодический) или близкий к нему переходный процесс (рис. 1.26, а, кривые 1 и, соответственно, 2);

 - слабоколебательный переходный процесс (рис. 1.26, б);

 - сильноколебательный переходный процесс (рис. 1.26, в).

          Отличие сильноколебательного от слабоколебательного переходного процесса заключается в количестве периодов колебаний (более 2-3 для сильноколебательного переходного процесса).

          Величина перерегулирования σ_п определяется как отношение величины  максимального выброса () к установившемуся значению ,

выраженное в процентах (рис. 1.26, б):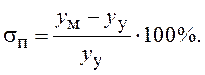 

          Для оценки величины перерегулирования с помощью метода ЛХ используют эмпирическое выражение: