Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 7

          На рис. 1.11 показаны  ЛХ усилительного звена. ЛАХ усилительного звена представляет собой горизонтальную прямую, проведенную на уровне  Около ЛАХ принято указывать наклон характеристики (в данном случае:  0 дБ на октаву или 0 дБ/окт). Главное достоинство метода анализа СУ с помощью ЛХ заключается в простоте их построения, не требующего применения вычислительных средств. Рекомендуется приближенное построение ЛАХ, использующее один из вариантов аппроксимации:

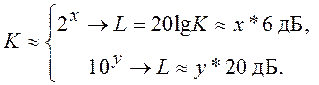
          Если для аппроксимации K используются степени 2, то погрешность построения ЛАХ не превысит 3 дБ. Такая погрешность вполне допустима для приближенного построения ЛАХ.

          ЛФХ усилительного звена также представляет собой горизонтальную прямую, но проведенную на уровне 0^о.

            Годограф усилительного звена вырождается в точку на вещественной оси, поскольку ПФ не зависит от частоты.

2. Интегрирующее звено (рис. 1.12).

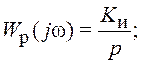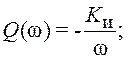
          ПФ и частотные характеристики интегрирующего звена:              P(ω)=0;  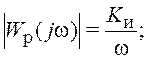         φ(ω)=-90^o.

          При одинаковой размерности входной и выходной величин коэффициент усиления интегрирующего звена имеет размерность [с^-1]. Поведение ЛАХ описывается выражением:

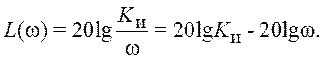
          Первое слагаемое графически отображается в виде горизонтальной прямой (усилительное звено), второе – в виде наклонной прямой, проходящей через начало координат и имеющей наклон -6 дБ/окт. В результате суммирования получается наклонная прямая, смещенная по оси ординат на величину (вверх, если K_и>1, и вниз, если K_и<1). ЛФХ интегрирующего звена представляет собой горизонтальную прямую, проведенную на уровне -90^о (на всех частотах выходное гармоническое колебание отстает по фазе от входного на 90^о).  На рис. 1.13 показаны ЛХ интегрирующего звена. Анализируя вид ЛХ, нетрудно представить поведение АФХ (рис. 1.14): модуль с ростом частоты уменьшается (годограф стремится к началу координат), ФЧХ постоянна, следовательно, АФХ интегрирующего звена совпадает с отрицательной мнимой полуосью.

3. Дифференцирующее звено (рис. 1.15).

          ПФ и частотные характеристики дифференцирующего звена: W_р(jω)=K_дjω;      P(ω)=0;     Q(ω)= K_дω;      φ(ω)=90^o.

          Идеальное дифференцирующее звено физически нереализуемо. При одинаковой размерности входной и выходной величин коэффициент усиления дифференцирующего звена K_д имеет размерность [с]. Поведение ЛАХ описывается выражением:

которое графически отображается прямой, имеющей наклон 6 дБ/окт и смещенной по оси ординат на величину . ЛФХ дифференцирующего звена представляет собой горизонтальную прямую, проведенную на уровне 90^о. На рис. 1.16 показаны ЛХ дифференцирующего звена. Модуль ПФ дифференцирующего звена с ростом частоты неограниченно увеличивается (годограф удаляется от начала координат), фазовая ЧХ звена постоянна: АФХ дифференцирующего звена совпадает с положительной мнимой полуосью (рис. 1.17).

          4. Апериодическое звено (рис. 1.18).

          ПФ и частотные характеристики апериодического звена:

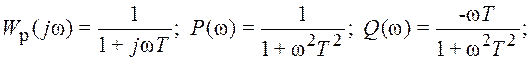
          Параметром звена является постоянная времени T.  Обратная величина ω_с=1/T называется частотой сопряжения. Поведение ЛАХ описывается выражением:

          Как уже отмечалось, главным достоинством метода анализа СУ с помощью ЛХ заключается в простоте их построения. Поэтому строится асимптотическая ЛАХ, представляющая собой ломаную линию. В нашем случае

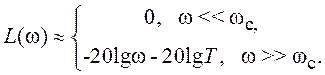
          Асимптотическая ЛАХ (рис. 1.19) состоит из 2-х асимптот, к которым стремится точная ЛАХ при и . Первая (низкочастотная) асимптота представляет собой горизонтальную прямую, совпадающую с осью абсцисс. Вторая (высокочастотная) асимптота представляет собой прямую, имеющую наклон  -6дБ/окт и смещенную по оси ординат на величину -20lgT.  Обе асимптоты пересекаются в точке ω=1/T=ω_с (отсюда и происходит название параметра ω_с – частота сопряжения). Наибольшее отличие асимптотической  ЛАХ от точной имеет место при ω=ω_с и это отличие примерно составляет 3 дБ (ранее отмечалось, что такая погрешность вполне допустима для приближенного построения ЛАХ). Асимптотическая и точная  (штриховая линия) ЛАХ апериодического звена показаны на рис. 1.19. При построении ЛФХ также не забывается главное достоинство метода ЛХ. Поэтому вместо функциональной зависимости φ(ω)=-arctg(ωT) строится приближенная зависимость φ^*(ω) (см. Табл. 1.1). На частоте ω=ω_с имеем φ(ω)= φ^*(ω)=-45⁰. При   а при   Задача выбора аппроксимирующей функции φ^*(ω) заключается в простом построении кривой, соединяющей две асимптоты (при  и ) и проходящей через точку φ(ω_с)=-45⁰.