Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 12

          При описании СУ во временной области снимаются ограничения, имеющие место в частотной области: возможно описание систем с переменными параметрами при ненулевых начальных условиях. Это обстоятельство существенно расширяет возможности анализа рассматриваемых систем. Например, описание и анализ систем с конечным временем съема данных, содержащих линейный ключ (см. гл. 8), возможно только во временной области.

          Еще более существенные преимущества временной области проявляются при использовании метода пространства состояний (ПС), позволяющего при описании СУ заменить дифференциальное уравнение n-го порядка системой из n дифференциальных уравнений первого порядка. Широкое применение метода ПС для описания и анализа динамических систем совпало во времени с внедрением ЭВМ. Наличие средств численного решения систем линейных и нелинейных дифференциальных уравнений предопределило большую популярность метода ПС. Весьма полезным оказалось еще одно обстоятельство: благодаря методу ПС для оптимизации систем радиоавтоматики удается использовать результаты теории оптимальной нелинейной фильтрации марковских случайных процессов, разработанные Р.Л. Стратоновичем (1960 г.). Наконец, описание в ПС распространяется на случай систем с несколькими входами, что оказывается весьма полезным при описании комплексных систем (см. разд. 6).

          Пусть СУ описывается дифференциальным уравнением n-го порядка:

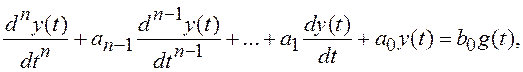                        (1.6)

с начальными условиями

,

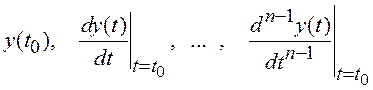где a₀,…,a_n-1 и b₀ – некоторые коэффициенты (не обязательно постоянные).

          С целью упрощения изложения существа метода рассматривается частный случай: в правой части дифференциального уравнения отсутствуют производные g(t) и a_n=1. Начальные условия дифференциального уравнения (1.6) могут быть и ненулевыми.

          С формальной точки зрения, дифференциальное уравнение (1.6) может быть изображено в виде структурной схемы, содержащей цепочку интеграторов и соответствующий набор усилительных звеньев с коэффициентами a₀,…,a_n-1 и b₀. Такую схему можно использовать для моделирования СУ с помощью аналоговой ЭВМ. При решении уравнения (1.6) с помощью цифровой ЭВМ это уравнение представляют в виде системы дифференциальных уравнений 1-го порядка.

          Используем новые переменные y₁(t), y₂(t),…, y_n(t) такие, что  

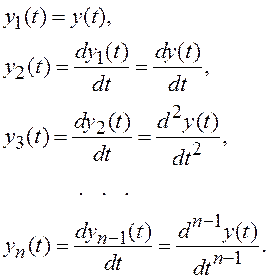                                                                        (1.7)

          Тогда уравнение (1.6) с учетом (1.7) записывается следующим образом:

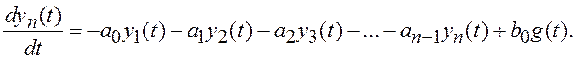                 (1.8)

Используя уравнения (1.7) и (1.8), можно получить матричную форму записи дифференциального уравнения (1.6):

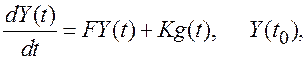                                      (1.9)                                                                       

где  - вектор состояния системы («T» - оператор транспонирования); Y(t₀) – состояние системы в момент времени t=t₀ (начальные условия);

;      

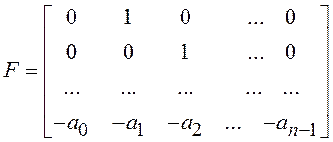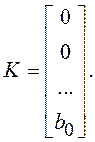
          Для установления связи между выходной переменной y(t) и вектором состояния Y(t) используется уравнение наблюдения:

                                                              (1.10)

          В соответствии с (1.7)  , следовательно

          Уравнение состояния системы (1.9) и уравнение наблюдения (1.10) определяют описание системы в пространстве состояний (ПС).

          В качестве примера дадим описание в ПС колебательного звена. Передаточной функции колебательного звена 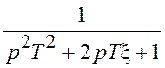  соответствует дифференциальное уравнение второго порядка:

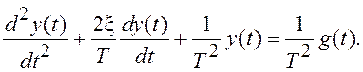
          Определяем компоненты вектора состояния:

При этом описание колебательного звена в ПС имеет следующий вид:

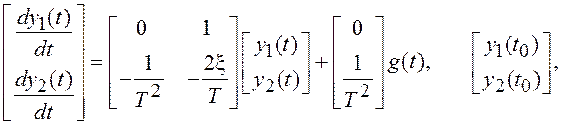
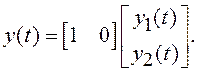
          В заключение заметим, что при выборе компонент вектора состояния системы существует некоторый произвол, поэтому описание систем в ПС неоднозначно: для одной и той же системы (с единственной ПФ) возможны разные наборы матриц F, K и H.

1.9. Описание СУ в пространстве состояний по передаточной функции