Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 14

Определим вектор состояния системы Y(t) с помощью компонент:                                     

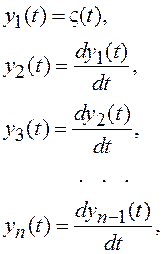
причем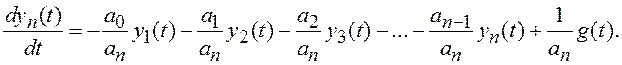                       

          Тогда уравнение состояния системы принимает вид:

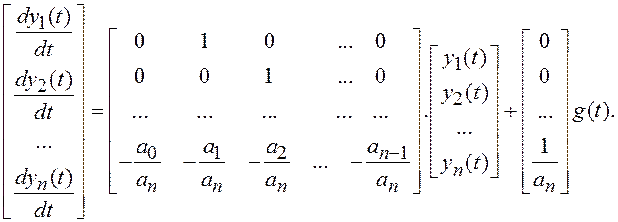
          ПФ  используем для составления уравнения наблюдения. Из второго уравнения системы (1.11) следует:

поэтому

,

где .

          Поскольку , матрица H в уравнении наблюдения дополняется нулями, количество которых равно (n-m-1).

          Для проверки правильности решения задачи следует по описанию системы в ПС составить структурную схему и для нее определить ПФ, которая должна совпасть с исходной. Формальные способы решения задачи приводят к сложным структурным схемам, что затрудняет выполнение проверки. Рассмотренный выше способ обладает дополнительным недостатком: уравнение наблюдения оказывается излишне сложным (удобнее такое описание в ПС, при котором одна из компонент вектора состояния Y(t) совпадает с выходной переменной y(t)).

          В качестве примера рассмотрим задачу описания в ПС СУ с ПФ в разомкнутом состоянии 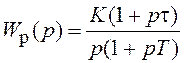. Сначала применим рассмотренный ранее способ описания системы в ПС с помощью структурной схемы. Используя эквивалентные структурные преобразования для апериодического и форсирующего звеньев, составляем структурную схему, содержащую только интегрирующие и усилительные звенья (рис. 1.30). Выходы интегрирующих звеньев обозначаем с помощью переменных вектора состояния: 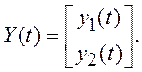  Обратим внимание на то, что первая компонента вектора состояния Y(t) на рис. 1.30 совпадает с выходной переменной y(t). Компоненты Y(t) можно поменять местами, но при этом получим другое описание системы в ПС.

          Входы интегрирующих звеньев определяют поведение производных компонент Y(t) в соответствии с дифференциальными уравнениями (записываются по структурной схеме, изображенной на рис. 1.30):

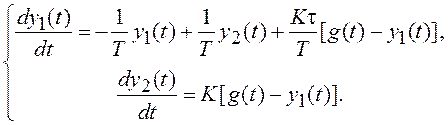
          Матричная форма записи этих уравнений соответствует уравнению состояния системы:

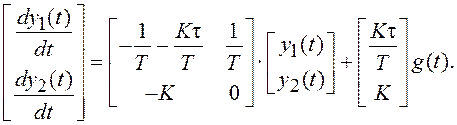                             (1.12)

          Уравнение состояния дополняется уравнением наблюдения:

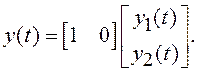                                                        (1.13)

          Заметим, что описание системы в ПС с помощью структурной схемы можно сначала составлять без учета обратной связи, полагая входной величиной e(t) с последующей заменой:

          Теперь применим рассмотренный ранее формальный способ решения задачи. С целью упрощения решения, не станем обращаться к ПФ замкнутой СУ, полагая, что входной величиной является не g(t), а e(t)=g(t)-y(t).

          Введем вспомогательную переменную ς(t) такую, что

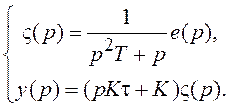                                                  (1.14)

Первому уравнению системы (1.14) соответствует дифференциальное уравнение:

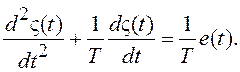                                                     (1.15)

          Определим вектор состояния системы

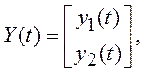    причем  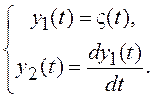                                   (1.16)

Дифференциальное уравнение (1.15) в новых переменных принимает вид:

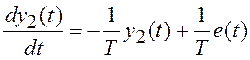
или, с учетом (1.16), в матричной форме:

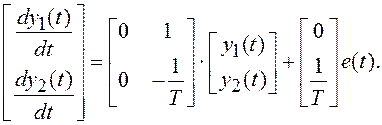                              (1.17)

Уравнение наблюдения:

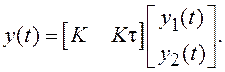                                                               (1.18)

Далее следует учесть наличие в СУ обратной связи. Вместо e(t) в уравнение (1.17) подставляем

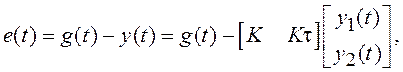
объединяем слагаемые, содержащие вектор состояния Y(t) и получаем окончательное выражение для уравнения состояния системы:

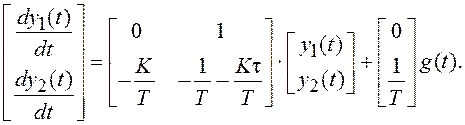                                (1.19)

          Полученные уравнения состояния (1.19) и наблюдения (1.18) отличаются от полученных ранее выражений (1.12) и (1.13).

1.10. Формирующий фильтр

Проектирование СУ начинается с выбора модели входного воздействия, представляющей собой математическое описание динамики изменения процесса g(t). Для описания входного воздействия обычно используется формирующий фильтр. Таким образом, формирующим фильтром называют линейную систему, вырабатывающую (формирующую) входное воздействие для СУ.

          Для формирования регулярных процессов применяется формирующий фильтр с ненулевыми начальными условиями при отсутствии входного сигнала. Заметим, что описание формирующего фильтра с ненулевыми начальными условиями, моделирующего регулярное воздействие, возможно только во временной области.