1.13. Простейший дискретный эквивалент системы управления
При нахождении простейшего дискретного эквивалента СУ решение
ВДУ (1.33) рассматривается на интервале временной дискретизации Δt=ti+1-ti с заменой t0 на ti и t
на ti+1. Для воздействия g(η)
используем аппроксимацию кусочно-постоянной функцией времени: ![]() либо
либо ![]() Такая аппроксимация справедлива при
достаточно малом интервале временной дискретизации и полезна при вычислении
интеграла в (1.33). Переходную матрицу представляем в виде матричной экспоненты,
которую раскладываем в ряд, оставляя в нем лишь первые два слагаемых (также
используется предположение о малости Δt). В результате имеем
Такая аппроксимация справедлива при
достаточно малом интервале временной дискретизации и полезна при вычислении
интеграла в (1.33). Переходную матрицу представляем в виде матричной экспоненты,
которую раскладываем в ряд, оставляя в нем лишь первые два слагаемых (также
используется предположение о малости Δt). В результате имеем
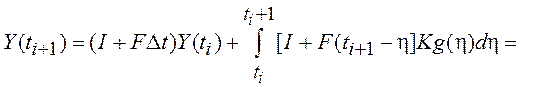
![]() (1.42)
(1.42)
Полученное выражение (1.42)
представляет собой векторное разностное уравнение, описывающее поведение
дискретной СУ – дискретного эквивалента непрерывной системы (1.33). Из
сопоставления (1.33) и (1.42) следует, что выражение в прямоугольных скобках в
правой части (1.42) равно скорости изменения вектора состояния непрерывной СУ Y(t), вычисленной в момент времени ti. Следовательно, выражение (1.42)
описывает алгоритм численного интегрирования Эйлера (метод прямоугольников).
Известно, что алгоритм Эйлера представляет собой простейший алгоритм численного
решения систем дифференциальных уравнений, поэтому выражение (1.42) описывает
поведение простейшего дискретного эквивалента непрерывной СУ (1.33). Заметим,
что выражение (1.42) легко получается непосредственно из (1.33) заменой 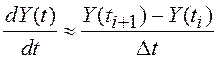 .
.
Условие эквивалентности систем (1.33) и (1.42)
следует из теоремы Котельникова: ![]()
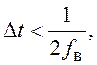 где fв – наивысшая спектральная составляющая воздействия g(t). На практике это условие проверяется с помощью
соотношения, связывающего интервал временной дискретизации Δt и время нарастания переходного
процесса tн:
где fв – наивысшая спектральная составляющая воздействия g(t). На практике это условие проверяется с помощью
соотношения, связывающего интервал временной дискретизации Δt и время нарастания переходного
процесса tн: 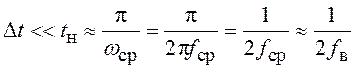 ( интересующая нас СУ должна
воспроизводить воздействие g(t), поэтому ее частота среза fср соизмерима с fв).
( интересующая нас СУ должна
воспроизводить воздействие g(t), поэтому ее частота среза fср соизмерима с fв).
В случае если структура СУ согласована со структурой формирующего фильтра и выполняется условие F=A-KH, выражение (1.42) принимает вид:
![]() (1.43)
(1.43)
(выражение (1.43) записано для аппроксимации ![]() ).
).
Воспользуемся выражением (1.43) для определения
простейшего дискретного эквивалента СУ с ПФ в разомкнутом состоянии ![]() . В соответствии с результатами разд.
1.11, такая система безошибочно воспроизводит постоянное воздействие g(t)=d,
для которого формирующий фильтр описывается дифференциальным уравнением 1-го
порядка:
. В соответствии с результатами разд.
1.11, такая система безошибочно воспроизводит постоянное воздействие g(t)=d,
для которого формирующий фильтр описывается дифференциальным уравнением 1-го
порядка:
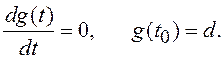
Следовательно, A=0 и H=1. Подстановка этих значений в (1.43) дает результат:
![]() (1.44)
(1.44)
Структура дискретной системы, описываемой скалярным разностным уравнением (1.44), показана на рис. 1.36, а и содержит дискретный интегратор (элемент задержки, охваченный единичной положительной обратной связью).
В разд. 1.11 определена структура непрерывной СУ, безошибочно воспроизводящей линейно изменяющееся воздействие g(t)=Vt. Найдем простейший дискретный эквивалент такой системы:
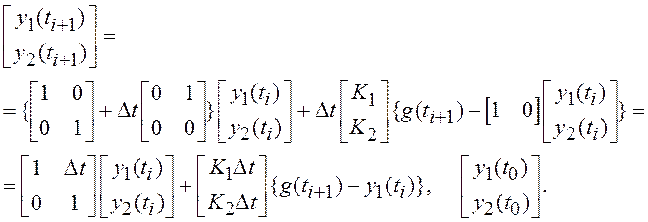 (1.45)
(1.45)
Заметим, что полученное разностное уравнение (1.45)
описывает алгоритм линейной экстраполяции 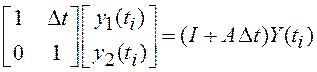 (первое слагаемое в правой части (1.45))
с последующей коррекцией результата экстраполяции с помощью сигнала
рассогласования
(первое слагаемое в правой части (1.45))
с последующей коррекцией результата экстраполяции с помощью сигнала
рассогласования ![]() , умноженного на весовые
коэффициенты (второе
слагаемое в правой части (1.45)). Сигнал рассогласования иногда формируют более
сложным способом с использованием результата экстраполяции:
, умноженного на весовые
коэффициенты (второе
слагаемое в правой части (1.45)). Сигнал рассогласования иногда формируют более
сложным способом с использованием результата экстраполяции: ![]() Такое формирование
Такое формирование ![]() формально получается при синтезе оптимальной
структуры дискретной системы, согласованной с дискретным эквивалентом
формирующего фильтра, содержащего 2 интегратора (см. гл. 5). В нашем примере:
формально получается при синтезе оптимальной
структуры дискретной системы, согласованной с дискретным эквивалентом
формирующего фильтра, содержащего 2 интегратора (см. гл. 5). В нашем примере: ![]() Структура такой дискретной СУ показана на рис. 1.36, б.
Структура такой дискретной СУ показана на рис. 1.36, б.
В некоторых случаях (например, если предположение о
малости Δt не выполняется) при разложении
матричной экспоненты в ряд полезно сохранить большее число слагаемых. Так, если
ФФ содержит 3 интегратора и 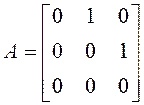 , вместо линейной экстраполяции
, вместо линейной экстраполяции ![]() в согласованной СУ можно использовать
параболическую экстраполяцию:
в согласованной СУ можно использовать
параболическую экстраполяцию: 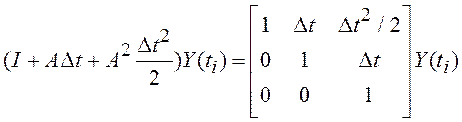 . Также, при нахождении дискретного
эквивалента можно использовать вытекающее из (1.38) при замене t0 на ti и t
на ti+1 разностное уравнение:
. Также, при нахождении дискретного
эквивалента можно использовать вытекающее из (1.38) при замене t0 на ti и t
на ti+1 разностное уравнение:
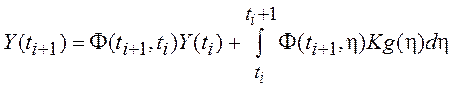 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.