Наличие в СУ обратной связи требует обеспечения ее устойчивости: работоспособная СУ безусловно должна быть устойчивой. Устойчивость линейной СУ – характеристика бинарная (система либо устойчива, либо неустойчива). В нелинейных системах возможно существование незатухающих автоколебаний при сохранении работоспособности. В случае возникновения проблем, связанных с устойчивостью СУ, решается задача коррекции. При этом добавляются специальные корректирующие элементы с целью улучшения технических характеристик СУ.
На начальном этапе работы СУ, как правило, протекает переходный процесс, при котором ОУ переходит из начального в установившееся состояние. Желательно, чтобы этот процесс протекал быстро и, по возможности, монотонно (иногда допускается слабоколебательный переходный процесс). Качество переходного процесса СУ зависит от степени удаления ее от границы устойчивости (от запаса устойчивости).
Точность СУ характеризуется ошибкой воспроизведения задающего воздействия в установившемся режиме работы. Если ошибка воспроизведения постоянного задающего воздействия (G=const) равна нулю, то СУ называют астатической (альтернатива – статическая СУ).
Задача обеспечения требуемой помехоустойчивости СУ возникает при наличии возмущающих воздействий (например, F1 на рис. 1.1). В устройствах радиотехнического назначения, т.е. системах радиоавтоматики, часто задающее воздействие G поступает на вход ЧЭ в аддитивной смеси с помехой, которую обычно аппроксимируют белым шумом (причиной возникновения такой помехи, как правило, являются тепловые шумы входных цепей радиоприемного устройства). Помехоустойчивость СУ иногда определяют по минимальному отношению сигнал/помеха, при котором еще сохраняются заданные технические характеристики системы. Более общей характеристикой помехоустойчивости СУ является дисперсия флюктуационной (обусловленной действием помехи) составляющей ошибки воспроизведения задающего воздействия. Очевидно, чем меньше эта дисперсия при заданном отношении сигнал/помеха, тем выше помехоустойчивость СУ.
1.2. Передаточные функции СУ
Решение задачи определения показателей качества СУ основывается на исследовании математических моделей, описание которых возможно в частотной и временной областях. В первом случае используются передаточные функции (ПФ) системы (ее математической модели), во втором – дифференциальные уравнения.
Определим ПФ СУ с помощью преобразования Лапласа:
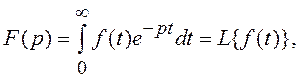
где f(t) – функция времени (оригинал); F(p) – изображение функции f(t) по Лапласу; L{·} – оператор преобразования Лапласа (L-1{·} – оператор обратного преобразования Лапласа).
Описание систем в частотной области сопровождается рядом ограничений, происхождение которых обязано преобразованию Лапласа и его свойствам. Напомним основные свойства преобразования.
1. Свойство линейности:
![]()
где a1 и a2 - некоторые коэффициенты, не зависящие от времени.
Из свойства линейности следует серьезное ограничение на описываемую систему: в частотной области возможно описание систем с постоянными параметрами. Для описания систем с переменными параметрами передаточные функции использовать, в общем случае, нельзя.
2. Изображение производной от оригинала
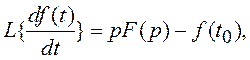
где f(t0) – значение функции f(t) в нуле (начальное условие).
Применение преобразования Лапласа к дифференциальным уравнениям обычно выполняется в предположении о нулевых начальных условиях и, соответственно, при описании систем с помощью ПФ также используется это предположение.
3. Изображение интеграла от оригинала
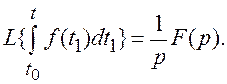
Это свойство полезно для обоснования обозначения интегратора на структурной схеме (рис. 1.5, а).
4. Смещение оригинала во времени
![]()
В дискретных системах присутствует элемент задержки, который будем обозначать так, как показано на рис. 1.5, б.
5. Конечное (предельное) значение оригинала
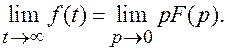
Это свойство преобразования Лапласа окажется полезным при анализе точности СУ.
Рассмотрим СУ со скалярным воздействием g(t) и реакцией y(t). Допустим, что известно описание СУ во временной области в виде дифференциального уравнения n-го порядка:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.