Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 15

В качестве примера на рис. 1.31 показано формирование полиномиального воздействия g(t)=d+Vt+at²/2 (параболы) с помощью фильтра, содержащего три интегратора. Определим переменные вектора состояния формирующего фильтра так, чтобы первая компонента g₁(t) совпадала с выходной переменной g(t). Тогда уравнения состояния формирующего фильтра, описывающего параболу, примут вид:

; ; ; ; ; .

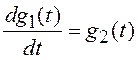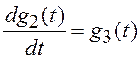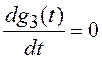          В матричном виде уравнения формирующего фильтра равны

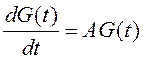; ; ,                                                        (1.20)

где ; ; .

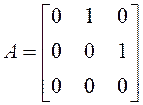          Уменьшая размерность вектора состояния формирующего фильтра, показанного на рис. 1.31, нетрудно получить линейное (g(t)=Vt) и постоянное (g(t)=d) воздействия. Воздействия вида: g(t)= d, Vt, at²/2, … в дальнейшем будем называть типовыми регулярными воздействиями.

          Для формирования случайных процессов (рис. 1.32) применяется формирующий фильтр (ФФ) с воздействием в виде белого шума u(t) с нулевым средним и заданной спектральной плотностью мощности шума S₀ (имеется в виду двусторонняя спектральная плотность мощности шума). Структура формирующего фильтра выбирается так, чтобы на выходе получить коррелированный случайный процесс (стационарный или нестационарный), адекватно отражающий реальное воздействие.

          Описание формирующего фильтра, моделирующего случайное воздействие, возможно в частотной и временной областях. В первом случае задается передаточная функция W_Ф(jω), при этом  и W_Ф(jω) полностью определяют спектральную плотность мощности   и автокорреляционную функцию R_g(τ) процесса g(t). Во втором случае для описания формирующего фильтра применяется метод пространства состояний. Поведение вектора состояния формирующего фильтра G(t) определяется векторным дифференциальным уравнением состояния

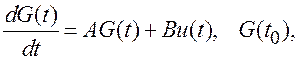                                      (1.21)

а связь процесса g(t) с вектором состояния G(t) определяет уравнение наблюдения  g(t) = HG(t). Матрицы A, B и H зависят от структуры и параметров ФФ, а также от выбора вектора состояния G(t).

          Рассмотрим наиболее часто встречаемые в инженерной практике модели случайных воздействий.

1. Экспоненциально-коррелированный случайный процесс (формирующий фильтр содержит апериодическое звено).

В частотной области этот  процесс (в установившемся режиме работы фильтра) характеризуется спектральной плотностью мощности

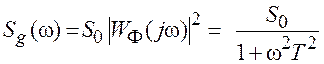
и автокорреляционной функцией

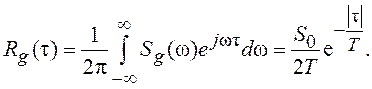                            (1.22)

          Во временной области данный процесс определяется решением дифференциального уравнения

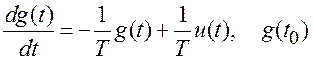                                  (1.23)

в виде: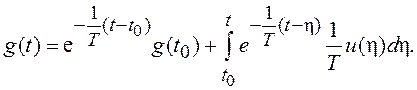    

          Важно отметить, что характеристики процесса во временной области определяются как в переходном режиме, так и в установившемся режиме работы фильтра.

 Автокорреляционная функция процесса легко вычисляется:

                ,

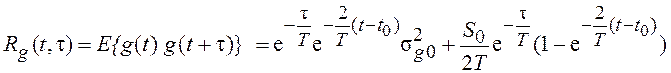где  - дисперсия случайной величины .

          Нетрудно убедиться, что результат вычислений в установившемся режиме работы фильтра (при t→∞ и τ>0) совпадает с выражением (1.22).

2. Винеровский процесс (формирующий фильтр содержит интегрирующее звено).

          Данная модель позволяет описывать нестационарные случайные процессы. В частотной области нестационарность винеровского процесса следует из вида спектральной плотности мощности

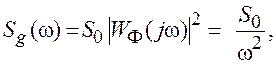                                         (1.24)

которая претерпевает разрыв при ω=0. Во временной области данный процесс определяется решением дифференциального уравнения

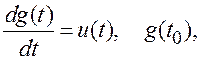                                                     (1.25)

которое при g(t₀)=0 имеет вид: 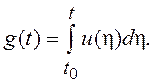   Дисперсия винеровского процесса   бесконечно нарастает с ростом времени, что также свидетельствует о его нестационарности.

3. Случайный процесс, скорость которого моделируется в виде экспоненциально-коррелированного процесса (формирующий фильтр содержит включенные последовательно апериодическое и интегрируюшее звенья).

          Скорость моделируемого процесса характеризуется дисперсией 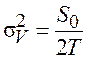   и интервалом корреляции T.