Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 5

  Частотная передаточная функция системы полностью определяет прохождение гармонического колебания через систему: АЧХ определяет зависимость амплитуды выходного колебания от частоты (при постоянной и равной единице амплитуде входного колебания), ФЧХ – фазовый сдвиг между выходным и входным колебаниями как функцию частоты.

  На рис. 1.7, а показан вид АЧХ, а на рис. 1.7, б – ФЧХ для 2-х замкнутых систем, имеющих ПФ в разомкнутом состоянии: 

              СУ 1: 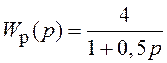    и  СУ 2:  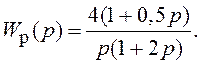           (1.5)

          По виду АЧХ нетрудно сделать некоторые выводы относительно показателей качества СУ. Во-первых, АЧХ системы 2 имеет резонансный пик, что свидетельствует о колебательном характере переходного процесса. АЧХ системы 1 не имеет резонансного пика, что свидетельствует о монотонном характере переходного процесса. Во-вторых, полоса системы 2 уже, следовательно, переходный процесс в этой системе протекает медленнее, чем в системе 1. В-третьих, вблизи нулевой частоты значение АЧХ системы 1 отличается от единицы, следовательно, эта  система воспроизводит постоянное задающее воздействие с ошибкой, т.е. это статическая система. Значение АЧХ системы 2 при  стремится к единице – это астатическая система.

          Весьма важным для анализа систем является следующее обстоятельство: СУ представляет собой фильтр нижних частот (ФНЧ), причем вид АЧХ и ФЧХ, при , определяет точность СУ, а вид АЧХ и ФЧХ, вблизи верхней границы полосы пропускания ФНЧ, определяет динамические характеристики системы (качество переходного процесса). Широкое использование частотных характеристик в инженерной практике началось с публикаций работ Г. Найквиста (1932 г.), А.В. Михайлова (1938 г.), Г. Боде (1945 г.) и других авторов.

Частотные характеристики могут быть изображены графически на комплексной плоскости в виде годографа. При построении годографа используются либо прямоугольные координаты P(ω) и Q(ω), либо полярные –  и φ(ω). Годограф называют также амплитудно-фазовой характеристикой (АФХ). Годограф, соответствующий ПФ разомкнутой СУ называют годографом Найквиста. Вид годографов Найквиста для 2-х СУ с ПФ (1.5) показан на рис. 1.8.

          Для статической системы 1 годограф начинается (при ) на положительной вещественной полуоси, а заканчивается (при ) в начале координат (направление роста частоты ω указывается стрелкой, иногда годограф снабжается частотными отметками).

При  ФЧХ СУ приближается к уровню, кратному 90^о, поэтому касательная к годографу в начале координат должна совпадать с одной из осей. Для астатических СУ модуль частотной передаточной функции при  стремится к бесконечности (вещественной или мнимой), поэтому годографы Найквиста для статической и астатической СУ существенно отличаются друг от друга (отличие АЧХ на рис. 1.7 при  заметно лишь при небольшом коэффициенте усиления СУ). Динамические  характеристики систем зависят от места пересечения годографом единичной окружности. Таким образом, свойства СУ определяются поведением годографа при  и вблизи единичной окружности, и это обстоятельство часто используется для приближенного построения годографа Найквиста.

          С учетом четности P(ω) и нечетности Q(ω) годограф Найквиста для отрицательных частот представляется в виде зеркального изображения годографа для положительных значений частоты относительно вещественной оси.

При проектировании и исследовании СУ очень удобно использовать логарифмические характеристики (ЛХ), что объясняется простотой их построения (ЛХ иногда называют диаграммами Боде). ЛХ состоит из 2-х графиков: логарифмической АЧХ (ЛАХ) и логарифмической ФЧХ (ЛФХ). Вид ЛХ для 2-х СУ с ПФ (1.5) показан на рис. 1.9 (рис. 1.9а – ЛАХ, рис. 1.9б – ЛФХ).

Правила построения ЛАХ:

1) по оси абсцисс откладывается частота ω в логарифмическом масштабе; в качестве основания логарифма используют 2 (октавное разбиение оси частот) для узкополосных систем и 10 (декадное разбиение оси частот) – для широкополосных; поскольку большинство систем радиоавтоматики относится к узкополосным системам, рекомендуется октавное, а не декадное разбиение оси частот;