Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 8

                                                                                                                         Табл. 1.1

          Используется прием деления отрезков пополам: от частоты сопряжения ω_с отступаем влево на октаву и делим отрезок размером 45⁰ пополам, отступаем влево еще на октаву и делим отрезок размером 22,5⁰ пополам и т.д. Дробные доли указаны в таблице для иллюстрации существа аппроксимации и при построении ЛФХ не учитываются. Правее частоты среза φ^*(ω) строится аналогичным образом. Ошибка аппроксимации не превышает 5⁰ и такая погрешность вполне допустима для приближенного построения ЛФХ. Точная φ(ω) и приближенная φ^*(ω) (отмечена точками) зависимости для апериодического звена показаны на рис. 1.19.

          Анализируя поведение ЛХ, легко представить вид АФХ: начало годографа (ω=0) находится на положительной вещественной полуоси в точке 1; далее, с ростом частоты, модуль уменьшается до 0, а фазовая ЧХ стремится к -90^о, следовательно, конец годографа () оказывается в начале координат, причем касательная к годографу при   совпадает с мнимой осью (рис. 1.20).   

          Очевидно,      или  

Это уравнение окружности с радиусом  1/2 и центром на положительной вещественной полуоси в точке 1/2. Частоте сопряжения соответствует точка годографа:   

         5. Форсирующее звено (рис. 1.21).

ПФ и частотные характеристики форсирующего звена:                   

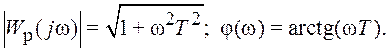
          Параметром звена является постоянная времени T.  Обратная величина ω_с=1/T называется частотой сопряжения.       Звено физически нереализуемо. ЛХ форсирующего звена являются зеркальным отображением ЛХ апериодического звена относительно оси абсцисс (рис. 1.22). Правила построения асимптотической ЛАХ и аппроксимации φ^*(ω) остаются прежними.      Годограф форсирующего звена похож на годограф дифференцирующего звена, но смещен по вещественной оси на 1.

          6. Колебательное звено (рис. 1.23).

          ПФ колебательного звена: 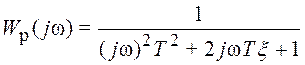.  Параметры колебательного звена: T – постоянная времени, ω_о=1/T – частота собственных колебаний звена, ξ – коэффициент затухания.

          Появление колебательных звеньев в СУ нежелательно и требует принятия мер для обеспечения условия  (в этом случае полюсы ПФ колебательного звена вещественны). Нетрудно убедиться, что при  ПФ колебательного звена представляется в виде произведения ПФ 2-х апериодических звеньев с разными (при ) или одинаковыми (при ) постоянными времени. На рис. 1.24 показан характер переходных процессов, возникающих в колебательном звене при воздействии единичной ступенчатой функции 1(t).

          При  переходный процесс имеет колебательный характер, при  - монотонный, с большой длительностью. Для СУ приемлемой оказывается ситуация, соответствующая : колебания демпфированы, а длительность переходного процесса относительно невелика. Для сравнения на рис. 1.24 показан также переходный процесс на выходе апериодического звена (кривая АЗ) с постоянной времени T=0,5с.

          ЛХ колебательного звена (при ) получаются сложением соответствующих характеристик 2-х апериодических звеньев с постоянной времени T.

1.5. Определение показателей качества СУ

 с помощью логарифмических характеристик