Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 16

          В инженерной практике возможно использование и более сложных моделей случайных воздействий. Например, последовательное включение в формирующем фильтре  апериодического звена и двух интегрируюших звеньев позволяет получить случайный процесс, ускорение которого моделируется в виде экспоненциально-коррелированного процесса. Ниже приведен наиболее распространенный вариант описания такого ФФ (описание систем в пространстве состояний неоднозначно):

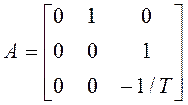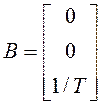                  ,          ,         .             (1.26)

          Ускорение моделируемого процесса характеризуется дисперсией 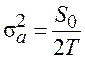   и интервалом корреляции T. В некоторых случаях дополнительно, с целью обоснованного выбора , конкретизируется плотность распределения вероятности ускорения p(a). Например, при описании динамики летательных аппаратов используется следующее предположение: ускорение с вероятностью p0 равно нулю, с вероятностью 2p1 максимально (того или другого знака), а в остальных случаях (с плотностью распределения вероятности 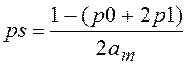)    принимает некоторое значение  из  заданного диапазона  [-a_m, a_m] (рис. 1.33).

    Для гражданских самолетов типовыми являются следующие параметры модели: a_m=g₀ (g₀ – ускорение свободного падения), p0=0,5 и p1=0,2. Дисперсия ускорения определяется по формуле:

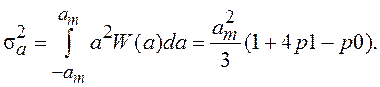
Интервал корреляции ускорения зависит от типа самолета: T=(20…60) с. Выбранные таким образом параметры модели полностью определяют спектральную плотность мощности белого шума на входе формирующего фильтра.

          Заметим, что скорость изменения g(t) в модели, соответствующей описанию ФФ (1.26), представляет собой нестационарный случайный процесс с неограниченно растущей дисперсией. Скорость реальных объектов ограничена, поэтому иногда соответствующий интегратор в ФФ охватывают местной отрицательной обратной связью с коэффициентом -1/τ и уравнение состояния ФФ имеет при этом вид: 

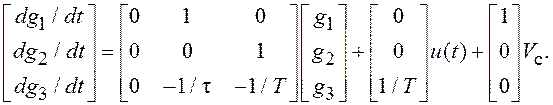                 (1.27)

Последнее слагаемое в правой части (1.27) учитывает регулярную составляющую скорости объекта V_C (в дополнение к стационарной случайной составляющей g₂(t)).

          Отметим, что рассмотренные модели случайных воздействий не исчерпывают многообразия ситуаций, встречающихся в инженерной практике. Иногда бывает полезно объединять процессы на выходах нескольких формирующих фильтров. Например, при проектировании системы синхронизации и использовании кварцевых генераторов с невысокой стабильностью частоты приходится учитывать быстрые флюктуации фазы («фазовый дребезг»). Можно включить параллельно два формирующих фильтра: один – для моделирования медленного дрейфа фазы гармонического сигнала, второй – для моделирования относительно быстрых флюктуаций фазы.

1.11. Задача идеального наблюдателя

          Найдем структуру такой СУ, которая безошибочно воспроизводит регулярное воздействие. Пусть известно описание формирующего фильтра в пространстве состояний:

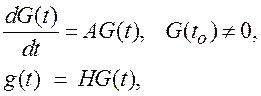                                           (1.28)

где G(t) – n-мерный вектор состояния формирующего фильтра вида: 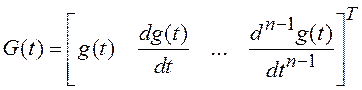; A –матрица, определяющая структуру и параметры формирующего фильтра; H =[1 0 … 0]– матрица наблюдения.

          Выход формирующего фильтра g(t) доступен для СУ (в канале наблюдения нет возмущений). Рассмотрим СУ, описание которой также дано в пространстве состояний:

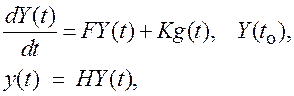                                           (1.29)

где Y(t) – n-мерный вектор состояния СУ вида: 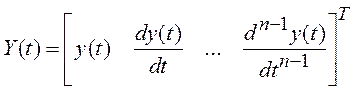; F и K – неизвестные пока матрицы.

          Требуем для  выполнения условий:

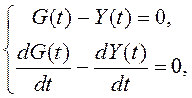                                                      (1.30)

которые обеспечивают безошибочное воспроизведение на выходе СУ воздействия g(t) (в каждый момент времени выполняется равенство g(t) и y(t), а также всех их производных до n-го порядка).

          Рассмотрим 2-е условие (1.30) с учетом уравнений состояния (1.28) и (1.29):

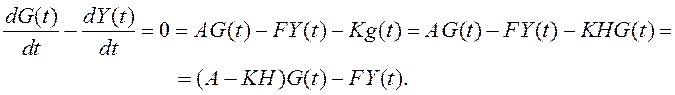
          Поскольку G(t)=Y(t), решение задачи идеального наблюдателя имеет вид:

F=A-KH.                                                                          (1.31)

          Подставим (1.31) в (1.29) и перегруппируем слагаемые:

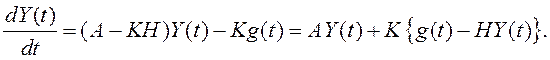              (1.32)

          Полученное уравнение (1.32) определяет структуру СУ, которая безошибочно воспроизводит заданное регулярное воздействие g(t). Структурная схема ФФ и системы, описываемой уравнением (1.32), показана на рис. 1.34 (двойные линии на рисунке обозначают векторные связи, интеграторы – многомерные).