При описании математической модели СУ целесообразно от функциональной перейти к структурной схеме, состоящей из набора типовых элементарных звеньев с указанием связей между ними. Решение такой задачи требует идентификации (т.е. определения) ПФ звеньев СУ. Если функциональный элемент состоит из резисторов, конденсаторов, операционных усилителей и т.п., то ПФ соответствующего звена нетрудно получить с помощью известных из электротехники законов Ома и Кирхгофа. Весьма часто, однако, функциональными элементами СУ являются управляемые генераторы, электродвигатели и редукторы, преобразователи различных типов и т.п. В такой ситуации для идентификации ПФ соответствующих звеньев рекомендуется использовать метод «черного ящика»: анализировать реакцию функционального элемента на пробные (тестовые) сигналы (δ-функция, единичная ступенчатая функция 1(t) и т.п.).
Формально задачу можно решить, применяя к реакции функционального элемента преобразование Лапласа. Для тестового сигнала вида δ(t)результат непосредственно дает ПФ звена, для тестового сигнала вида 1(t)результат необходимо умножить на p. Удобнее неформальное решение задачи идентификации, заключающееся в сопоставлении реакции тестируемого функционального элемента с известными реакциями типовых элементарных звеньев.
Рассмотрим подробнее этот способ на примере идентификации ПФ звеньев, соответствующих функциональным элементам системы фазовой автоподстройки частоты (ФАПЧ, рис. 1.28). В отличие от рассмотренной в разд. 1.1 функциональной схемы системы автоподстройки частоты здесь в качестве чувствительного элемента используется не частотный, а фазовый дискриминатор (ФД). Информационным параметром принимаемого радиосигнала является фаза φс и ФД преобразует разность фаз принимаемого радиосигнала и сигнала УГ φс-φг в напряжение. Остальные функциональные элементы остались без изменений, но добавлена корректирующая цепь (КЦ).
Начнем идентификацию ПФ с ФД. В качестве тестового сигнала будем использовать единичную ступенчатую функцию 1(t). Изменим скачком фазу принимаемого радиосигнала при неизменной фазе φг. Соответственно должно измениться напряжение на выходе ФД. Реальные элементы обычно инерционны, поэтому поведение ФД как динамической системы можно описать с помощью ПФ апериодического звена:
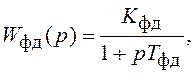
где Kфд– коэффициент усиления ФД (размерность: в/град); Tфд – постоянная времени ФД.
Заметим, что фаза (и угол) формально являются безразмерными физическими величинами, но в данном случае, для понимания существа дела, полезно рассматривать их как размерные величины.
В некоторых случаях инерционностью ФД можно пренебречь (в сравнении с инерционностью других функциональных элементов). Тогда поведение ФД как динамической системы можно описать с помощью ПФ усилительного звена:
Используемые в системах радиоавтоматики усилители малоинерционны, поэтому поведение усилителя можно также описать с помощью ПФ усилительного звена:
где Kу – коэффициент усилителя (безразмерный).
Корректирующая цепь в рассматриваемом аналоговом устройстве, как правило, состоит из резисторов и конденсаторов и ПФ такой цепи Wкц(p) нетрудно определить с помощью законов электротехники.
Варикап (управляемая напряжением емкость) практически безынерционен, поэтому
где Kв – коэффициент усиления варикапа (размерность пФ/в).
При идентификации ПФ УГ следует учесть, что его
реакцией в системе ФАПЧ является фаза выходного напряжения. Изменим скачком
емкость варикапа: изменится частота УГ ωг(t). Поскольку
частота и фаза связаны известным соотношением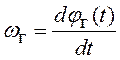 
или 
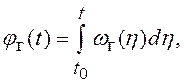поведение УГ следует описывать с помощью
ПФ интегрирующего звена:
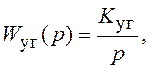
где Kуг – коэффициент усиления УГ (размерность град/с/пФ).
Заметим, что два функциональных элемента (варикап и УГ) в структурной схеме можно объединить:
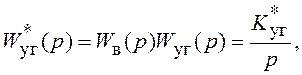
где 
- общий коэффициент усиления
варикапа и УГ (размерность град/с/в).
ПФ разомкнутой системы ФАПЧ определяется в результате перемножения ПФ перечисленных звеньев:
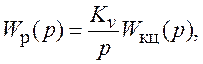
где Kv=KфдKуKвKуг ( размерность с-1).
1.8. Метод пространства состояний
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.