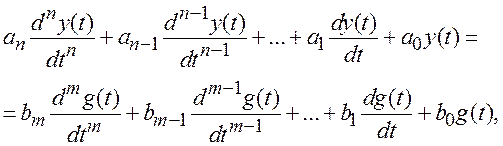Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 4

                          (1.1)

где a₀,…,a_n и b₀,…,b_m – постоянные коэффициенты.

Начальные условия дифференциального уравнения (1.1)

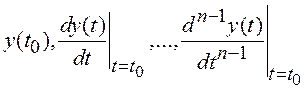
полагаем нулевыми. Применяем к уравнению (1.1) преобразование Лапласа:

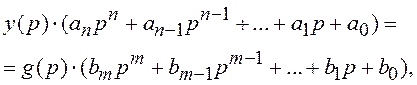
где y(p) и g(p) – изображения по Лапласу для y(t) и, соответственно, g(t).

  Определим ПФ СУ как отношение изображения по Лапласу реакции системы к изображению воздействия:

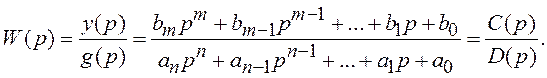                  (1.2)

Заметим, что возможно и другое определение ПФ системы: изображение по Лапласу реакции системы на δ-функцию, т.е. изображение весовой функции. Поскольку , такое определение ПФ не противоречит (1.2). Также отметим, что выражение (1.2) представляет собой дробную рациональную функцию.

  Рассмотрим некоторые общие свойства ПФ.

1. Из условия физической реализуемости системы следует ограничение: порядок многочлена числителя C(p) ПФ (1.2) не может превышать порядка многочлена знаменателя D(p), т.е.

2. При p=0 ПФ (1.2) превращается в коэффициент усиления

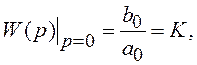
который для рассматриваемой СУ, в силу ее назначения, либо равен 1 (в астатических системах), либо близок к 1 (в статических системах).

3. ПФ (1.2) можно представить в виде:

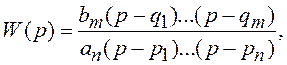
где q₁,…,q_m- корни многочлена C(p), называемые нулями; p₁,…,p_n - корни многочлена D(p), называемые полюсами ПФ.

  Обобщенную функциональную схему линейной СУ при скалярных воздействии g(t) и реакции y(t) можно заменить обобщенной структурной схемой (рис. 1.6).

          Обобщенная структурная схема отражает принцип управления по рассогласованию: разность задающего воздействия и реакции системы e(t)=g(t) – y(t) представляет собой сигнал ошибки или рассогласования СУ, который используется далее для решения основной задачи системы:  Кроме того, схема наглядно демонстрирует наличие отрицательной обратной связи в контуре управления. Учитывая наличие отрицательной обратной связи, замыкающей контур СУ, ПФ W(p)  в дальнейшем будем называть ПФ замкнутой СУ. Определим также ПФ разомкнутой СУ W_Р(p) и ПФ по ошибке W_e(p):

              

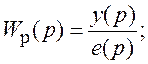
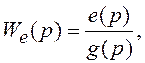
где y(p), e(p) и g(p) – изображения по Лапласу от y(t), e(t) и g(t).

          Все  ПФ однозначно связаны друг с другом. Для определения выражений, устанавливающих такую связь, необходимо записать уравнения СУ, следующие из обобщенной структурной схемы (рис. 1.6):

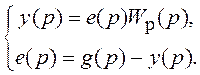                                                                                               (1.3)

Подстановка 2-го уравнения из системы (1.3) в 1-е позволяет записать:

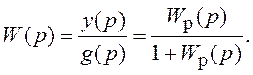                                                                                                (1.4)

Деление левой и правой частей 2-го уравнения из системы (1.3) на g(p) позволяет получить:

    а с учетом (1.4):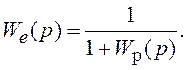   

  Любая из определенных здесь ПФ может использоваться для описания и анализа СУ. В инженерной практике, однако, ПФ замкнутой системы обычно используется для анализа устойчивости и помехоустойчивости, ПФ разомкнутой системы – для оценки качества переходных процессов, а ПФ по ошибке – для анализа точности СУ.

1.3. Частотные характеристики СУ

Частотная передаточная функция системы получается из передаточной функции W(p) заменой p=jω:

причем возможно использование любой из определенных в разд. 1.2 ПФ СУ.

Формально частотная передаточная функция представляет собой отношение изображения по Фурье реакции системы к изображению воздействия. Однако следует иметь в виду, что передаточная функция W(p) существует как для устойчивых, так и для неустойчивых систем, в то время как частотная передаточная функция W(jω) имеет смысл только для устойчивых систем.

          Являясь функцией комплексной переменной, W(jω) представима в алгебраической и показательной формах:

 

где P(ω) и Q(ω) – вещественная и мнимая частотные характеристики системы;  и φ(ω) – амплитудная и фазовая частотные характеристики системы (АЧХ и ФЧХ).

  Связь между 2-мя формами представления W(jω) устанавливают следующие соотношения:

      

      

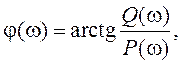
из которых следует что  и P(ω) – четные функции частоты, а φ(ω) и Q(ω) – нечетные.