Легко видеть, что структура формирующего фильтра полностью воспроизведена в составе СУ, поэтому такую СУ иногда называют согласованной. Полученный результат наглядно показывает, что структура СУ и, соответственно, сложность ее реализации зависят от динамики изменения отслеживаемого (оцениваемого) воздействия g(t).
В качестве примера решим задачу идеального наблюдателя для линейного воздействия g(t)=Vt. Формирующий фильтр и СУ имеют 2-й порядок, причем
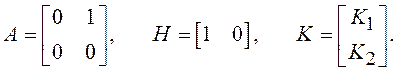
Из уравнения (1.32) следует структура согласованной СУ (рис. 1.35).
При нулевых начальных условиях (Y(t0)=0) в СУ возникает переходный процесс, по окончании которого ошибка воспроизведения g(t) стремится к нулю:
1.12. Аналитическое решение векторного дифференциального уравнения
Анализ регулярных процессов в СУ во временной области сводится к решению векторного дифференциального уравнения (ВДУ). Для этой цели обычно используются известные стандартные алгоритмы решения систем дифференциальных уравнений (например, алгоритм Рунге-Кутта). Здесь мы рассмотрим аналитическое решение ВДУ, которое окажется полезным в дальнейшем при нахождении дискретного эквивалента СУ и выводе дисперсионных уравнений.
Пусть СУ описана в ПС:
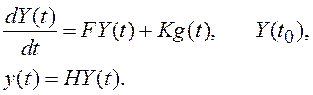(1.33)
Применим к (1.33) преобразование Лапласа:
(1.34)
(1.35)
где Y(p) – вектор, элементы которого представляют собой отображение по Лапласу элементов вектора состояния СУ Y(t).
Группируя в (1.34) слагаемые, содержащие Y(p), в левой части, получаем
где I – единичная матрица.
Полагая матрицу (pI-F) неособенной, находим
(1.36)
и возвращаемся во временную область, применяя обратное преобразование Лапласа:
Определим переходную матрицу
,
(1.37)
тогда
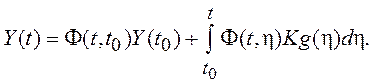(1.38)
Выражение (1.38) представляет собой аналитическое решение ВДУ. В случае g(t)=0 имеем решение однородного ВДУ:
причем переходная матрица Φ(t,t0) характеризует собственное движение системы (переход)
из состояния Y(t0) в состояние Y(t)
(отсюда и следует название матрицы). Для систем 1-го порядка такой переход
описывается экспонентой, поэтому переходную матрицу рассматривают как матричную
экспоненту (обобщение скалярной экспоненты): 
Такое представление удобно в случае
возникновения трудностей с вычислением переходной матрицы по формуле (1.37).
Тогда используется разложение матричной экспоненты в ряд:
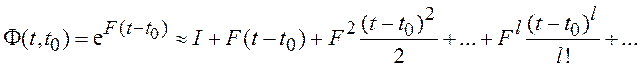. (1.39)
Очевидно следующее свойство переходной матрицы:
.
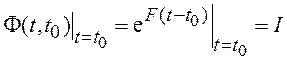Кроме того, переходная матрица удовлетворяет исходному ВДУ:
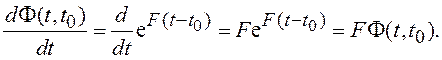(1.40)
Перечисленных свойств переходной матрицы вполне достаточно для проверки результата (1.38). С этой целью используем метод подстановки (дифференцируем (1.38)):
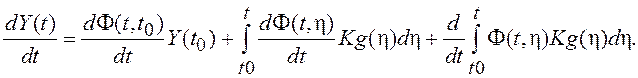
Во втором слагаемом правой части (1.38) присутствуют две функции времени: Φ(t,η) и интеграл с переменным верхним пределом интегрирования. В соответствии с правилом Лейбница производная от интеграла с переменным верхним пределом интегрирования равна подынтегральному выражению, вычисленному в точке верхнего предела интегрирования. С учетом перечисленных свойств переходной матрицы имеем
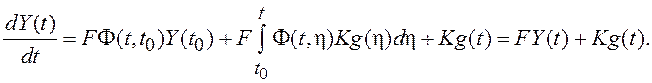
Получили исходное ВДУ, что подтверждает результат (1.38).
В разд. 1.9 рекомендована связь описаний систем в частотной и временной областях через структурную схему. Такая связь позволяет без существенных проблем переходить от описания систем с помощью ПФ к описанию в ПС и обратно. Существует другой способ решения задачи перехода от описания систем в ПС к описанию с помощью ПФ. Пусть Y(t0)=0. Из (1.35) и (1.36) имеем
В соответствии с определением ПФ замкнутой системы получаем следующий результат:
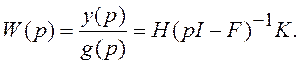(1.41)
Полученное соотношение, справедливое для дробной рациональной ПФ, окажется полезным в дальнейшем при анализе устойчивости систем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.