Системы радиоавтоматики, их классификация и показатели качества. Частотные характеристики СУ. Типовые элементарные звенья СУ и их логарифмические характеристики, страница 10

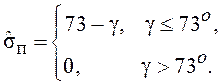
          Время нарастания переходного процесса t_н – временной интервал от начала переходного процесса до первого пересечения установившегося уровня, если такое пересечение существует (рис. 1.26, в). Для монотонного переходного процесса пересечение отсутствует и время нарастание определяют через постоянную времени T экспоненциального процесса: (кривая 1на рис. 1.26, а,).

          Для оценки времени нарастания переходного процесса с помощью метода ЛХ используют эмпирическое выражение:

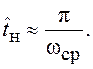
          Таким образом, при оценивании качества переходного процесса СУ с помощью ЛХ определяются степень колебательности (по величине γ), величина перерегулирования (по величине γ) и время нарастания (по величине ω_ср). Далее строится примерная осциллограмма переходного процесса. В нашем примере , следовательно, переходный процесс слабоколебательный; ; рад/с, с.

          Точность СУ зависит от наклона низкочастотной асимптоты ЛАХ и величины коэффициента усиления. Помехоустойчивость СУ зависит от частоты среза и величины запаса устойчивости по фазе. Вопросы анализа точности и помехоустойчивости СУ рассматриваются в гл. 3.

1.6. Соединение звеньев СУ

          Для построения ЛХ используется ПФ разомкнутой системы . Эта ПФ определяется по структурной схеме, отражающей набор типовых элементарных звеньев системы и их взаимосвязи. Общий метод решения задачи определения  по заданной структурной схеме связан с введением вспомогательных переменных и составлении уравнений системы с последующим исключением вспомогательных переменных. Однако для большинства практических задач достаточно знать типовые соединения, которые здесь и рассматриваются (с пояснением общего метода решения задачи).

          1. Последовательное соединение (рис. 1.27, а).

          Вводим вспомогательную переменную f(t) и для изображений по Лапласу g(p), f(p) и y(p) записываем уравнения системы, состоящей из 2-х последовательно соединенных звеньев:

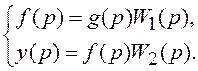
Подстановкой 1-го уравнения во 2-е исключаем вспомогательную переменную f(t):

Далее используем определение ПФ:

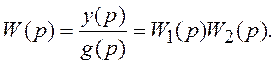
          Таким образом, ПФ последовательного соединения звеньев равна произведению их ПФ.

          2. Параллельное соединение (рис. 1.27, б).

          Вводим вспомогательные переменные f₁(t) и f₂(t) и составляем уравнения системы:

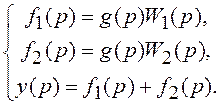
Подстановкой первых 2-х уравнений в 3-е исключаем вспомогательные переменные f₁(t) и f₂(t):

откуда получаем:

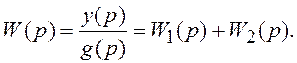
          Следовательно, ПФ параллельного соединения звеньев равна сумме их ПФ.

          3. Включение звена в цепи отрицательной обратной связи (рис. 1.27, в).

          Вводим вспомогательную переменную f(t) и составляем уравнения системы:

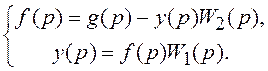
Подстановкой 1-го уравнения во 2-е исключаем вспомогательную переменную f(t):

откуда получаем:

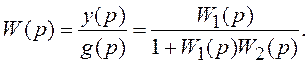
          Заметим, что аналогичная задача решалась в разделе 1.2 при выводе соотношения, связывающего ПФ замкнутой и разомкнутой СУ. Кроме того, обратим внимание на то обстоятельство, что для положительной обратной связи (сумматор на входе соединения) в знаменателе  появится знак минус.

          При включении звена в цепи обратной связи иногда используется терминология: жесткая или гибкая обратная связь. Термин «жесткая обратная связь» применяется в ситуации, когда ПФ звена в цепи обратной связи удовлетворяет условию: Такая обратная связь действует и в переходном, и в установившемся режимах работы системы. Термин «гибкая обратная связь» применяется в ситуации, когда в цепи обратной связи включаются дифференцирующие звенья и . Такая обратная связь действует только в переходном режиме работы системы.

          Конечно, рассмотренные типовые соединения не исчерпывают всего многообразия форм взаимосвязи звеньев и, в сложных ситуациях, рекомендуется обращаться к общему методу решения задачи. В отдельных случаях оказываются полезными эквивалентные структурные преобразования (изменения структурной схемы, не приводящие к изменению ПФ). Некоторые из таких преобразований будут рассмотрены далее.

1.7. Идентификация передаточной функции звена СУ

          В задаче определения ПФ СУ, рассмотренной в разд. 1.6, структурная схема предполагалась известной. Теперь рассмотрим задачу построения структурной схемы СУ.