Описание СУ обычно начинают с идентификации ПФ
звеньев и вычисления ПФ разомкнутой системы ![]() . Если анализ системы предполагается
проводить во временной области, то следует решить задачу перехода от описания
системы с помощью ПФ к описанию в ПС. Существует несколько формальных способов
решения такой задачи для произвольного вида ПФ. Общим недостатком этих способов
является сложность выполнения проверки правильности описания системы в ПС. Для
СУ, структура которых состоит из типовых элементарных звеньев, возможен и более
удобный способ решения задачи: описание СУ в ПС по структурной схеме.
. Если анализ системы предполагается
проводить во временной области, то следует решить задачу перехода от описания
системы с помощью ПФ к описанию в ПС. Существует несколько формальных способов
решения такой задачи для произвольного вида ПФ. Общим недостатком этих способов
является сложность выполнения проверки правильности описания системы в ПС. Для
СУ, структура которых состоит из типовых элементарных звеньев, возможен и более
удобный способ решения задачи: описание СУ в ПС по структурной схеме.
Сначала рассмотрим более удобный для СУ способ описания в ПС по структурной схеме системы. В основу этого способа заложена главная идея метода ПС: состояние системы в каждый момент времени определяют значения элементов памяти, характеризуемые компонентами вектора состояния. В непрерывной системе элементами памяти являются интеграторы, поэтому следует по ПФ составить структурную схему, содержащую только усилительные и интегрирующие звенья. Далее выходы интегрирующих звеньев обозначают через компоненты вектора состояния системы, входы интегрирующих звеньев определяют поведение производных этих компонент. Остается по структурной схеме записать уравнения состояния и наблюдения.
Для составления структурной схемы используется ПФ
разомкнутой СУ ![]() , которая, в большинстве случаев, представляет собой
произведение ПФ типовых элементарных звеньев. Среди этих звеньев встречаются
апериодическое и форсирующее звенья, для которых необходимо применить эквивалентные
структурные преобразования (эквивалентными называются такие преобразования структуры,
которые не меняют ПФ звена).
, которая, в большинстве случаев, представляет собой
произведение ПФ типовых элементарных звеньев. Среди этих звеньев встречаются
апериодическое и форсирующее звенья, для которых необходимо применить эквивалентные
структурные преобразования (эквивалентными называются такие преобразования структуры,
которые не меняют ПФ звена).
1.Преобразование структуры апериодического звена.
Представим ПФ апериодического звена в виде:
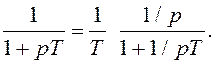
Такому представлению ПФ, согласно содержанию разд. 1.6, соответствует структурная схема, показанная на рис. 1.29, а. Схема содержит интегратор (элемент памяти) и два усилительного звена.
2. Преобразование структуры форсирующего звена при наличии интегратора.
Очевидное преобразование ПФ последовательного соединения форсирующего звена и интегратора:
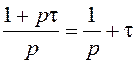
приводит к структурной схеме с параллельным включением интегратора и усилительного звена (рис. 1.29, б).
3. Преобразование структуры форсирующего звена при наличии апериодического звена (такое преобразование рекомендуется использовать для описания в ПС статических СУ).
Параллельное соединение усилительного звена K1
и апериодического звена 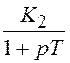 имеет ПФ:
имеет ПФ:
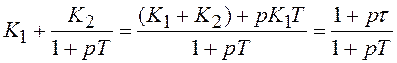
при выполнении условий: ![]()
Эквивалентная структурная схема для последовательного соединения апериодического и форсирующего звеньев приведена на рис. 1.29, в.
4. Преобразование структурной схемы соединения с дифференцирующим звеном в цепи обратной связи.
В составе некоторых СУ встречается
электромеханический привод (например, в следящем измерителе угловых координат
положением антенны обычно управляет электродвигатель). С целью улучшения
характеристик такого привода с ПФ 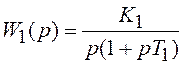 применяют тахометрическую обратную
связь, включая в цепи обратной связи звено с ПФ вида
применяют тахометрическую обратную
связь, включая в цепи обратной связи звено с ПФ вида 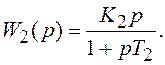
Представим ПФ соединения в виде:
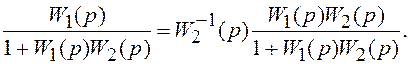
Такому представлению соответствует структурная схема, показанная на рис.
1.29, г. ПФ ![]() представляет последовательное
соединение форсирующего звена и интегратора, а произведение
представляет последовательное
соединение форсирующего звена и интегратора, а произведение ![]() является сочетанием форсирующего и
апериодического звеньев. Эквивалентное структурное преобразование таких элементов
рассмотрено выше. Таким образом наличие интегратора в
является сочетанием форсирующего и
апериодического звеньев. Эквивалентное структурное преобразование таких элементов
рассмотрено выше. Таким образом наличие интегратора в ![]() решает проблему избавления от
дифференцирующего звена в цепи, охваченной обратной связью.
решает проблему избавления от
дифференцирующего звена в цепи, охваченной обратной связью.
Теперь рассмотрим один из самых простых формальных способов описания СУ в ПС по ПФ.
Пусть система задана с помощью ПФ общего вида:
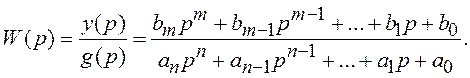
Введем вспомогательную переменную ς(t) такую, что
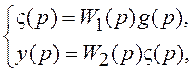 (1.11)
(1.11)
где ![]() ;
; 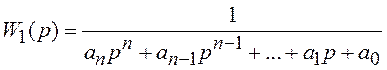 ;
;
![]() ;
; ![]()
Опишем систему с ПФ ![]() в ПС известным нам способом (см. разд. 1.8). Передаточной
функции
в ПС известным нам способом (см. разд. 1.8). Передаточной
функции ![]() соответствует дифференциальное уравнение:
соответствует дифференциальное уравнение:
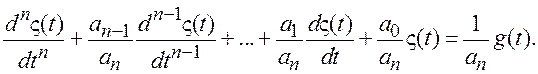
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.