Глава 5
Оптимизация систем радиоавтоматики
5.1. Параметрическая оптимизация
При проектировании следящих
измерителей с непрерывным временем частотными методами измеритель
рассматривается как линейная система, содержащая дискриминатор, сглаживающую
цепь с ПФ ![]() и цепь обратной связи (рис. 5.1, а).
Параметрическая оптимизация следящего измерителя заключается в оптимизации
параметров ПФ
и цепь обратной связи (рис. 5.1, а).
Параметрическая оптимизация следящего измерителя заключается в оптимизации
параметров ПФ ![]() при заданном воздействии
при заданном воздействии ![]() и известной спектральной плотности помехи
и известной спектральной плотности помехи ![]() . При этом характеристики дискриминатора
предполагаются фиксированными.
. При этом характеристики дискриминатора
предполагаются фиксированными.
Дискриминатор при рассогласованиях
в пределах линейного участка дискриминационной характеристики представляется
как линейный элемент c
коэффициентом усиления ![]() , а спектральная плотность мощности
сигнала (СПМ) ошибки на выходе дискриминатора пересчитывается в эквивалентную СПМ широкополосной
помехи на входе системы
, а спектральная плотность мощности
сигнала (СПМ) ошибки на выходе дискриминатора пересчитывается в эквивалентную СПМ широкополосной
помехи на входе системы ![]() . Затем с использованием
эффективной полосы
. Затем с использованием
эффективной полосы ![]() ПФ
ПФ ![]() выполняется
расчет дисперсии флюктуационной ошибки
выполняется
расчет дисперсии флюктуационной ошибки ![]() (рис. 5.1, б).
(рис. 5.1, б).
Количество интеграторов в
сглаживающей цепи выбирается исходя из выбранного вида типового воздействия.
Кроме сглаживающей цепи в передаточную функцию ПФ разомкнутого контура ![]() включают инерционные элементы
дискриминатора, двигателя и т. д.
включают инерционные элементы
дискриминатора, двигателя и т. д.
Оптимизация следящего
измерителя заключается в оптимизации параметров ![]() передаточной
функции
передаточной
функции ![]() при заданном воздействии и известной СПМ
помехи
при заданном воздействии и известной СПМ
помехи ![]() . Оптимизация выполняется по критерию
минимума среднего квадрата суммарной ошибки в установившемся режиме:
. Оптимизация выполняется по критерию
минимума среднего квадрата суммарной ошибки в установившемся режиме:
![]() ,
, ![]() .
(5.1)
.
(5.1)
Значение установившейся ошибки ![]() определяется в соответствии с
рекомендациями разделов 3.2 и 3.3, а расчет дисперсии флюктуационной ошибки
определяется в соответствии с
рекомендациями разделов 3.2 и 3.3, а расчет дисперсии флюктуационной ошибки ![]() – раздела 3.6.
– раздела 3.6.
Для нахождения оптимальных значений ![]() находится решение системы уравнений
находится решение системы уравнений
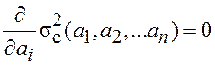 ,
, ![]() .
.
Рассмотрим простейший
пример параметрической оптимизации системы с одним интегратором, имеющей
передаточную функцию разомкнутого контура ![]() и ПФ
и ПФ 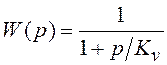 , при типовом воздействии с постоянной
скоростью
, при типовом воздействии с постоянной
скоростью ![]() и действии помехи с СПМ
и действии помехи с СПМ ![]() . Коэффициент усиления разомкнутого контура
. Коэффициент усиления разомкнутого контура
![]() включает коэффициенты усиления дискриминатора
и интегратора.
включает коэффициенты усиления дискриминатора
и интегратора.
Используя выражение
(3.21) и данные табл. 3.2, получим значение дисперсии флюктуационной ошибки ![]() . Полагая, что скорость изменения параметра
с равной вероятностью принимает значения
. Полагая, что скорость изменения параметра
с равной вероятностью принимает значения ![]() и
и ![]() , вычислим среднеквадратическое значение
скорости
, вычислим среднеквадратическое значение
скорости ![]() . Задаваясь этим значением и используя данные табл.3.1, получим
значение среднего квадрата установившейся ошибки
. Задаваясь этим значением и используя данные табл.3.1, получим
значение среднего квадрата установившейся ошибки ![]() .
.
Тогда выражение (5.1) принимает вид
![]() .
.
Выполняя
дифференцирование по ![]() , и приравнивая результат нулю,
получим уравнение для оптимального значения
, и приравнивая результат нулю,
получим уравнение для оптимального значения ![]() .
.
![]() , и
далее
, и
далее
![]() .
(5.2)
.
(5.2)
Средний квадрат суммарной ошибки при этом равен
![]() .
.
Рассмотрим еще один
важный пример параметрической оптимизации системы с двумя интеграторами,
имеющей передаточную функцию разомкнутого контура ![]() .
Ошибки создаются типовым воздействием
.
Ошибки создаются типовым воздействием ![]() и
помехой со спектральной плотностью
и
помехой со спектральной плотностью ![]() . Из табл. 3.2 получим
значение оптимальной эффективной полосы пропускания
. Из табл. 3.2 получим
значение оптимальной эффективной полосы пропускания ![]() , и
определим величину флюктуационной ошибки
, и
определим величину флюктуационной ошибки ![]() . Далее
с помощью табл.3.1 определим значение квадрата установившейся ошибки
. Далее
с помощью табл.3.1 определим значение квадрата установившейся ошибки ![]() . Вычислив производную квадрата суммарной
ошибки по
. Вычислив производную квадрата суммарной
ошибки по ![]() , получим алгебраическое уравнение для
определения оптимального коэффициента усиления.
, получим алгебраическое уравнение для
определения оптимального коэффициента усиления.
![]() и
затем
и
затем
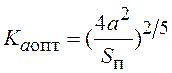 . (5.3)
. (5.3)
Средний квадрат суммарной ошибки равен
![]() .
.
При оптимальной полосе
пропускания ![]() , и система имеет малый запас устойчивости.
Для ускорения ввода в режим слежения можно увеличить запас устойчивости, выбрав
, и система имеет малый запас устойчивости.
Для ускорения ввода в режим слежения можно увеличить запас устойчивости, выбрав
![]() [РУ].
[РУ].
5.2. Параметрическая оптимизация систем с дискретным временем
Параметрическая
оптимизация систем с дискретным временем может выполняться частотными или
временными методами. Для исследования систем с постоянными параметрами можно
применить метод ![]() -преобразования, однако частотный
метод анализа достаточно прост лишь для простых полиномиальных воздействий.
Анализ систем во временной области также позволяет решить задачу определения
стационарных характеристик систем.
-преобразования, однако частотный
метод анализа достаточно прост лишь для простых полиномиальных воздействий.
Анализ систем во временной области также позволяет решить задачу определения
стационарных характеристик систем.
Выполним оптимизацию системы с одним дискретным интегратором, на вход которой поступает сумма воздействия с постоянной скоростью и дискретного белого шума (рис. 5.2).
Воздействие с постоянной скоростью формируется с помощью разностного уравнения
![]() ,
,
где ![]() ;
; 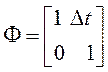 ;
; ![]() .
.
Начальное значение
скорости ![]() хранится в
хранится в ![]() и
является случайной величиной c нулевым средним и
среднеквадратическим значением
и
является случайной величиной c нулевым средним и
среднеквадратическим значением ![]() . Случайный шум в
уравнении формирующего фильтра отсутствует, и матрица
. Случайный шум в
уравнении формирующего фильтра отсутствует, и матрица ![]() .
.
Воздействие ![]() описывается уравнением
описывается уравнением
![]() ,
,
где ![]() –
матрица наблюдения процесса
–
матрица наблюдения процесса ![]() ;
; ![]() – дискретный белый шум наблюдения с
известной дисперсией
– дискретный белый шум наблюдения с
известной дисперсией ![]() .
.
Разностное уравнение системы с одним интегратором имеет вид
![]() ,
(5.4)
,
(5.4)
где ![]() – состояние интегратора;
– состояние интегратора; ![]() – коэффициент усиления системы.
– коэффициент усиления системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.