Оптимизация систем радиоавтоматики. Комплексные системы радиоавтоматики, страница 15

            Комплексная обработка сигналов ГНСС и ИНС является актуальной проблемой из-за широкого применения ГНСС. Рассмотрим принцип измерения координат объекта с помощью спутников. При измерении положения объектов используется геодезическая система координат, начало которой расположено в центре Земли (рис. 6.11). Ось  лежит на пересечении плоскости экватора и плоскости Гринвичского меридиана, ось  проходит через Северный полюс, а ось  направлена так, чтобы система координат была правой. Определение координат объекта  основано на измерении задержек распространения сигналов между объектом и спутниками, координаты которых ,  известны благодаря информационным сообщениям. При измерении задержек принятых сигналов используется шкала времени потребителя, которая может иметь сдвиг времени  относительно шкалы времени спутниковой системы. Влияние погрешности временной шкалы устраняется с помощью использования избыточных измерений, и для измерения трех координат и сдвига времени производится прием не менее четырех сигналов спутников.  Современные приемники принимают сигналы всех видимых в данный момент спутников (от 6 до 11 спутников системы).

            Строим систему на основе принципа инвариантности с использованием автономных данных о проекциях скорости объекта ,  и . Ошибки измерения скорости моделируем как экспоненциально-коррелированный процесс. Случайное изменение трех координат полагаем независимым и для каждой координаты составляем уравнения подобные (6.23). Кроме того, добавляем в систему два уравнения, моделирующих изменение сдвига часов потребителя  из-за нестабильности задающего генератора. Для этой цели используем уравнения вида (3.28), заменив в них обозначения  на  и  на . Размер вектора состояния системы  при этом равен восьми.

            Уравнение состояния имеет вид:

,                                                        (6.35)

где ;

;

, при этом

 ; ; ; ; .

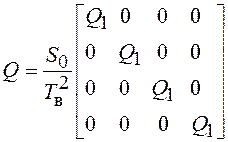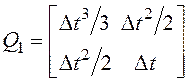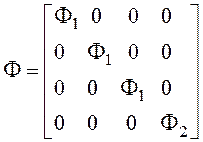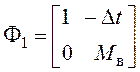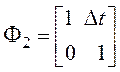            Матрицы в уравнении (6.35) составлены из блоков, взятых из уравнений (3.26), (3.27) и (6.24).

            Если в качестве наблюдаемого вектора взять  выходных сигналов измерителей, следящих за задержкой кода, получим комплексную систему со слабой интеграцией. Вектор наблюдения имеет вид:

,                                               (6.36)

где  – -мерная функция;  – число принимаемых спутников;  – вектор дискретного белого шума с известной  диагональной корреляционной матрицей.

            -тая строка функции  , называемая псевдодальностью -того спутника, равна:

,      (6.37)

где   – скорость света;  – дальность от объекта до -того спутника.

Оценку комплексной обработки  получаем с помощью расширенного фильтра Калмана. Для этого находим производную нелинейной функции  в точке :

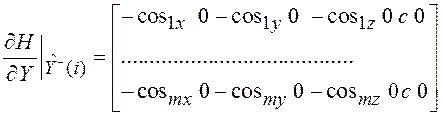,                              (6.38)

где ,  и  – направляющие косинусы отрезка, соединяющего объект и -тый спутник; ;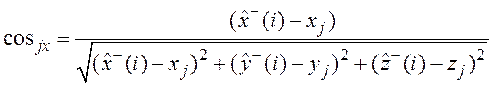

;.

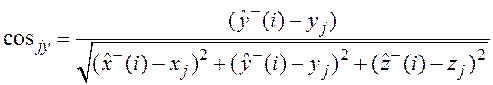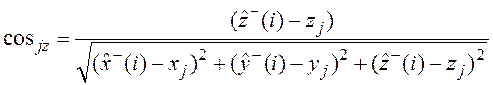            Далее с помощью выражений (5.41 – 5.46) определяем оптимальный коэффициент усиления и составляем уравнение фильтрации.

.                                       (6.39)

            Рассмотрим структуру разности . -тая строка разности имеет вид , и представляет собой разность между измеренным и прогнозируемым значениями псевдодальности. Экстраполированные значения составляющих вектора  вычисляются с помощью уравнения экстраполяции.

.                                                      (6.40)

            Автономные данные, используемые при экстраполяции, содержатся в слагаемом .

Для прогноза используются результаты экстраполяции вектора состояния и координаты спутника , полученные с помощью так называемого эфемеридного расчета. Расчет координат спутника основан на  данных, содержащихся в информационном сообщении этого спутника.

 Используя выражения (6.39) и (6.40) построим структурную схему фильтра (рис. 6.12). В этой схеме автономные данные не используются в измерителях задержки для повышения их помехоустойчивости. При кратковременном подавлении радиосигналов помехами комплексный фильтр переходит в режим экстраполяции с использованием автономных данных. Точность определения координат в комплексном фильтре будет выше, чем в автономной системе, так как составляющие автономной скорости в фильтре  корректируются поправками ,  и .

6.9. Измерение задержки сигналов при глубокой интеграции ГНСС и ИНС