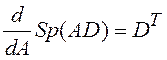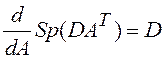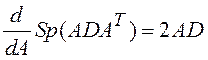Другие предметы \ Основы автоматики и систем автоматического управления

Оптимизация систем радиоавтоматики. Комплексные системы радиоавтоматики, страница 4

, , .

После вычисления градиента корреляционной матрицы из (5.15) получаем и оптимальное значение коэффициента .

. (5.16)

Подстановка оптимального значения в выражение (5.15) позволяет найти минимальное значение корреляционной матрицы ошибки.

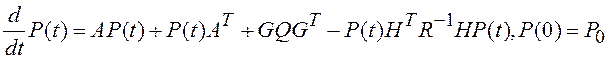. (5.17)

Выражения (5.14), (5.16) и (5.17) определяют алгоритм оптимального фильтра в непрерывном времени (рис. 5.8). Матрицы для сокращения записи представлены как постоянные величины, но при численном решении дифференциальных уравнений они могут быть функциями времени. Выражение (5.17) является матричным дифференциальным уравнением Рикатти. Это уравнение нелинейное и в общем случае решается численными методами.

Рассмотренный алгоритм был получен и исследован американским ученым Калманом и носит его имя. Если матрица и шумы и имеют гауссовское распределение, то этот алгоритм является оптимальным в классе линейных и нелинейных алгоритмов.

5.5. Линейный фильтр Калмана в дискретном времени

При численном решении дифференциальных уравнений выполняется дискретизация во времени. Используя представление случайных процессов в дискретном времени с помощью разностных уравнений, можно упростить цифровую аппаратную и программную реализацию оптимальных фильтров.

Составим разностные уравнения наблюдения случайного процесса в дискретном времени , являющиеся дискретным эквивалентом уравнений непрерывного времени (5.12) и (5.13).

, (5.18)

, (5.19)

где – -мерный вектор; – переходная матрица размером ; –-мерный вектор дискретного белого гауссовского шума с нулевым средним и корреляционной матрицей ; – -мерный вектор; – матрица размером ; – -мерный вектор дискретного белого гауссовского шума с нулевым средним и корреляционной матрицей .

Формирование векторов и показано на рис. 5.9,а.

В выражениях (5.18) и (5.19) матрицы и для упрощения записи считаются постоянными, но при вычислительной реализации эти матрицы могут быть функциями дискретного времени.

При проектировании оптимального фильтра предполагается, что на вход фильтра поступает вектор наблюдения , формируемый в соответствии с выражениями (5.18) и (5.19), а фильтр должен вырабатывать несмещенную оценку с минимальной среднеквадратичной ошибкой. Оценка формируется рекуррентным способом, и предполагается наличие известной оптимальной оценки и ее корреляционной матрицы .

В случае дискретного времени оценка выполняется в два этапа. На первом этапе формируется оценка экстраполяции на основе известной оценки для момента времени . На втором этапе фильтрации оценка экстраполяции оптимальным образом объединяется с наблюдением , полученным в момент времени .

Для нахождения оценки экстраполяции используем выражение (5.18). При отсутствии априорной информации оценка белого дискретного шума с гауссовским распределением равна его наиболее вероятному значению – нулю. Тогда из (5.18) получим

. (5.20)

Ошибка экстраполяции вычисляется из (5.18) и (5.20).

. (5.21)

Ошибка не коррелированна с шумом , так как она содержит лишь составляющие шума , и т. д. Тогда используя (5.21), получим значение корреляционной матрицы ошибок экстраполяции .