Оптимизация систем радиоавтоматики. Комплексные системы радиоавтоматики, страница 16

            Схема комплексирования с глубокой интеграцией отличается использованием автономных данных в измерителях задержки. Размер вектора состояния  как и выше равен восьми. Уравнение состояния построим из матриц, взятых из выражений (3.25), (3.34) и (6.22).

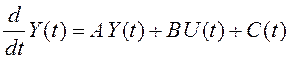,                                    (6.41)

где ;

;, при этом

; ; ; ; ; ; .

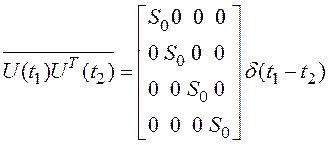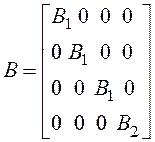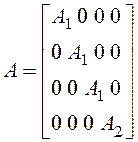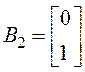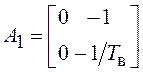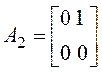Вектор наблюдения  составлен из  принятых радиосигналов.

,                                      (6.42)

где  – нелинейная функция, состоящая из  строк вида

;  – огибающая сигнала;  – частота высокочастотного заполнения; ;  – псевдодальность;  – -мерный вектор белого шума с диагональной корреляционной матрицей , заполненной спектральными плотностями .

Для построения оптимального фильтра необходимо выполнить линеаризацию нелинейной функции  . При линеаризации ошибка оценивания координат должна быть малой по сравнению с длительностью элемента огибающей и длительностью периода высокочастотного заполнения. Длительность элемента в каналах широкого доступа равна 1 мкс (GPS) или 2 мкс (Глонасс), и условие малой ошибки реализуется. Однако требование малой ошибки очень сложно выполнить для высокочастотного заполнения. Ошибка измерения должна составлять малую часть периода, и при длине волны радиосигнала  порядка 20 см это означает, что ошибка измерения расстояния должна составлять единицы сантиметров. Для достижения такой точности требуется выполнить сложную операцию устранения неоднозначности фазовых измерений. Поэтому для упрощения задачи ограничимся построением комплексного фильтра, объединяющего измерители задержки огибающей и автономные данные. После упрощения -тая строка нелинейной функции  и ее производная равны:

 и ,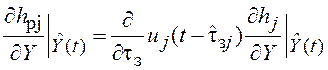

 где  .

            Выражение производной получено путем дифференцирования сложной функции, и содержит нелинейную функцию  из предыдущей задачи. Производные 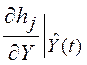 являются строками матрицы  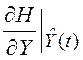из выражения (6.38).

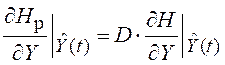,                                                 (6.43)

где  – диагональная матрица размером , в которой на диагонали стоят элементы .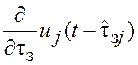

            Строим комплексный фильтр с помощью выражения (5.36).

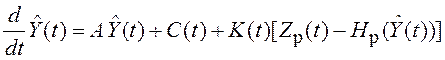.                           (6.44)                                             

Коэффициент усиления с учетом (6.43) равен:

.

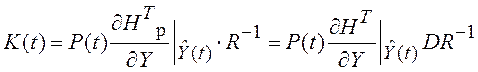Рассмотрим в выражении (6.44) произведение коэффициента усиления на разность.

.

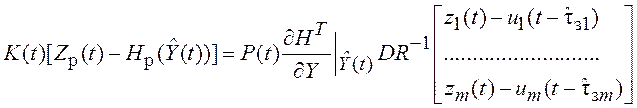            При перемножении матриц  и  на столбец разностей образуются произведения вида

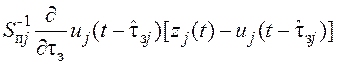.                            (6.45)

          Отметим, что подобное произведение производной на разность встречалось в формуле (5.37). В примере 5.3 показано, что при построении фильтра величину  (в квадратной скобке) можно не учитывать.

          Построим структуру оптимальной комплексной системы, используя выражения (6.43) и (6.45). В схеме фильтра принятые радиосигналы , содержащиеся в векторе , умножаются в соответствии с (6.45) на производные , задержанные на интервал  (рис. 6.13). При вычислении задержки используется оценка вектора состояния  и координаты спутника (), формируемые с помощью принимаемой со спутника информацией. Операция в выражении (6.45) может рассматриваться как выделение сигнала ошибки при измерении задержки принятого сигнала. Результаты измерения сигналов ошибок затем с помощью матричного коэффициента 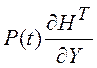 используются для коррекции оценки  . Автономные данные о скорости используются путем суммирования вектора .

Отличие схемы с глубокой интеграцией заключается в том, что оценка задержки  -того спутника формируется с использованием информации, получаемой от всех спутников и автономных данных. В схеме со слабой интеграцией следящие измерители работают независимо друг от друга. При кратковременном пропадании приема какого-либо спутника измеритель прекращает слежение. В схеме с глубокой интеграцией оценка  продолжает формироваться, что ускоряет повторный ввод в слежение.

Недостаток схемы с глубокой интеграцией заключается в большой вычислительной сложности. В схеме со слабой интеграцией частота дискретизации определяется шириной спектра сигнала на выходе следящего измерителя и составляет десятки или сотни Гц. При глубокой интеграции частота дискретизации зависит от ширины спектра радиосигнала и составляет десятки МГц. Частично проблема вычислительной сложности алгоритма фильтрации решается путем разделения фильтра на части, действующие с высокой и низкой частотой дискретизации.