Оптимизация систем радиоавтоматики. Комплексные системы радиоавтоматики, страница 11

Комплексирование системы позволяет снизить коэффициент усиления контура дальномера  и таким образом снизить полосу пропускания  и влияние флюктуационных помех. Другим важным свойством комплексной системы является сохранение формирования отсчета дальности  при кратковременном прерывании приема радиосигнала. Изменение отсчета  происходит благодаря интегрированию величины , которая близка к истинной скорости движения .

При полете в турбулентной атмосфере в измерениях датчика воздушной скорости наряду с постоянной ошибкой содержится случайная составляющая, имеющая функцию корреляции 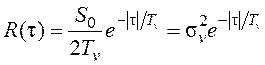, где  в зависимости от условий полета изменяется в пределах от 0,4 до 5,5 м/с, а  составляет единицы секунд. Спектральная плотность мощности флюктуаций равна .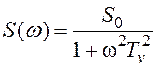

            При оптимальном выборе  ПФ  имеет вид 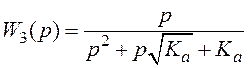 . Для расчета дисперсии динамической составляющей ошибки при случайном воздействии на систему используем результаты разд. 3.7. Дисперсия случайной ошибки  равна

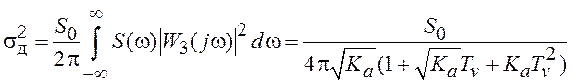.                 (6.10)                               

            Пример 6.2. Оценим выигрыш в помехоустойчивости комплексного дальномера. Полагаем, что помеха на входе дальномера имеет спектральную плотность  и ускорение объекта управления . При отсутствии комплексирования с помощью формулы (5.3) находим оптимальное значение  и дисперсию суммарной ошибки . В случае комплексирования полагаем, что среднеквадратическое значение ошибки измерения воздушной скорости  и . Результаты расчета дисперсий флюктуационной  и динамической  составляющих ошибки по формулам (3.22)

Табл. 6.1

и (6.10) в зависимости от значения  приведены в табл. 6.1. Можно видеть, что дисперсия суммарной ошибки  и оптимальное значение  при комплексировании снижаются, причем оптимальное значение   находится вблизи 0,01. Более точное определение параметров комплексной системы целесообразно выполнять, используя метод пространства состояний.

6.5. Использование временных методов при комплексировании

Комплексные системы могут строиться как с использованием информации о движении объекта, так и без нее на основе принципа инвариантности.

Рассмотрим способ комплексирования, основанный на использовании информации о движении объекта. Составим дифференциальные уравнения, описывающие движение объекта и изменение медленных составляющих ошибок измерительных устройств:

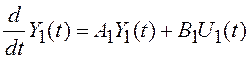,                                        (6.11)

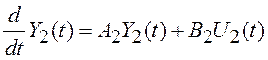,                                     (6.12)

где  – -мерный вектор состояния объекта;  – -мерный вектор состояния медленных составляющих ошибок;  – матрица размером ;  – вектор белого гауссовского шума размерности  с нулевым средним и  диагональной корреляционной матрицей ;  – матрица размером , .

            Процесс наблюдения описывается уравнением

,                             (6.13)

где  – -мерный вектор;  – матрица размером ,;  – -мерный белый гауссовский шум с нулевым средним и  корреляционной матрицей .

            Особенность выражения (6.13) заключается в том, что ошибки при измерении компонент вектора  являются суммой медленных ошибок  и белого шума .

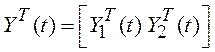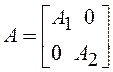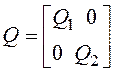            Составим вектор состояния комплексной системы , вектор шума , блочно-диагональные матрицы  и , матрицу 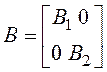, имеющую размер ,  и матрицу наблюдения . Тогда вместо уравнений (6.11), (6.12) и (6.13) получим уравнения модели воздействия в виде (5.18) и (5.19). Затем с помощью алгоритма фильтра Калмана найдем оптимальную оценку вектора состояния .

            Комплексная система получается сложной, так как размерность фильтра определяется суммой . Кроме того, для реализации оптимального алгоритма требуется иметь много априорных данных  – значения матриц , , , , ,  и .