![]() . (5.26)
. (5.26)
Существует и другой
вариант вычисления матрицы ![]() и оптимального
коэффициента
и оптимального
коэффициента ![]() .
.
![]() . (5.27)
. (5.27)
![]() .
(5.28)
.
(5.28)
Последний вариант
вычисления коэффициента ![]() используется на
практике редко, так как выражение (5.27) содержит три обращения матриц.
используется на
практике редко, так как выражение (5.27) содержит три обращения матриц.
Система уравнений (5.20), (5.22), (5.23), (5.25), и (5.26) определяют алгоритм оптимальной фильтрации Калмана в дискретном времени (рис. 5.9, б).
Особенность полученного
алгоритма заключается в том, что в каждый момент времени ![]() используются только значения оптимальной
оценки
используются только значения оптимальной
оценки ![]() и ее корреляционной матрицы
и ее корреляционной матрицы ![]() в предыдущий момент времени. Это свойство
объясняется тем, что процесс
в предыдущий момент времени. Это свойство
объясняется тем, что процесс ![]() является марковским
процессом.
является марковским
процессом.
Пример 5.2. Построим
фильтр Калмана для оптимального оценивания фазы генератора ![]() , в котором скорость изменения фазы
является винеровским процессом. Разностные уравнения формирующего фильтра (5.18)
в рассматриваемом случае имеют вид (3.28). Уравнение наблюдения (5.19) при
измерении фазы с ошибкой
, в котором скорость изменения фазы
является винеровским процессом. Разностные уравнения формирующего фильтра (5.18)
в рассматриваемом случае имеют вид (3.28). Уравнение наблюдения (5.19) при
измерении фазы с ошибкой ![]() принимает вид
принимает вид ![]() .
.
Из уравнения экстраполяции (5.20), используя выражения (3.26) и (3.28) получим
![]() и
и ![]() .
.
Определив коэффициент ![]() , из уравнения фильтрации (5.23) получим
систему уравнений.
, из уравнения фильтрации (5.23) получим
систему уравнений.
![]() ,
(5.29)
,
(5.29)
![]() .
(5.30)
.
(5.30)
Выражениям (5.29) и
(5.30) соответствует схема на рис. 5.10. Коэффициенты ![]() и
и
![]() должны вычисляться в соответствии с
выражениями (5.23), (5.26) и (5.27).
должны вычисляться в соответствии с
выражениями (5.23), (5.26) и (5.27).
Алгоритмы оптимальной
фильтрации позволяют минимизировать ошибки только при точном знании априорных
данных – матриц шумов ![]() и
и ![]() , а
также начального значения корреляционной матрицы
, а
также начального значения корреляционной матрицы ![]() . Если
значения матриц
. Если
значения матриц ![]() и
и ![]() реальных
процессов намного превышают значения, использованные при расчете коэффициента
усиления
реальных
процессов намного превышают значения, использованные при расчете коэффициента
усиления ![]() , может возникнуть расходимость фильтра, то
есть нарастание ошибок с течением времени. Для преодоления априорных трудностей
используют адаптивные алгоритмы фильтрации.
, может возникнуть расходимость фильтра, то
есть нарастание ошибок с течением времени. Для преодоления априорных трудностей
используют адаптивные алгоритмы фильтрации.
5.6. Оптимальная нелинейная фильтрация
В радиотехнических системах полезные
параметры (дальность, угловые координаты и т.д.) модулируются в принятом
радиосигнале нелинейным образом. Кроме того, навигационные параметры,
содержащиеся в наблюдаемой величине ![]() , во многих
радионавигационных системах связаны нелинейной зависимостью с вектором
состояния
, во многих
радионавигационных системах связаны нелинейной зависимостью с вектором
состояния ![]() , характеризующим положение и вектор
скорости объекта. В простейших расчетах предполагается, что дискриминатор
работает на линейном участке характеристики, и используется теория линейной
фильтрации. Однако для более точных расчетов необходимо использовать теорию
нелинейной фильтрации. Советский ученый Р.Л.Стратонович в 1960 г. получил
уравнение (которое носит его имя), описывающее изменение во времени
апостериорной плотности марковского процесса
, характеризующим положение и вектор
скорости объекта. В простейших расчетах предполагается, что дискриминатор
работает на линейном участке характеристики, и используется теория линейной
фильтрации. Однако для более точных расчетов необходимо использовать теорию
нелинейной фильтрации. Советский ученый Р.Л.Стратонович в 1960 г. получил
уравнение (которое носит его имя), описывающее изменение во времени
апостериорной плотности марковского процесса 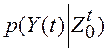 в
нелинейной системе (см. 7.8). Уравнение Стратоновича содержит частные
производные и его численное решение связано с большими трудностями. В линейном
случае из уравнения Стратоновича можно получить алгоритм фильтра Калмана. В
нелинейной системе плотность вероятности
в
нелинейной системе (см. 7.8). Уравнение Стратоновича содержит частные
производные и его численное решение связано с большими трудностями. В линейном
случае из уравнения Стратоновича можно получить алгоритм фильтра Калмана. В
нелинейной системе плотность вероятности 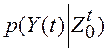 имеет
негауссовское распределение. Одним из подходов для получения приближенного
решения задачи нелинейной оптимальной фильтрации является гауссовская
аппроксимация апостериорной плотности. Приближенное решение может быть получено
также и методом линеаризации нелинейных зависимостей и последующим
использованием теории линейной фильтрации.
имеет
негауссовское распределение. Одним из подходов для получения приближенного
решения задачи нелинейной оптимальной фильтрации является гауссовская
аппроксимация апостериорной плотности. Приближенное решение может быть получено
также и методом линеаризации нелинейных зависимостей и последующим
использованием теории линейной фильтрации.
Найдем решение задачи нелинейной фильтрации для непрерывного времени с помощью линеаризации.
Уравнения случайного
процесса ![]() и наблюдения
и наблюдения ![]() в
отличие от выражений (5.12) и (5.13) содержат нелинейные зависимости
в
отличие от выражений (5.12) и (5.13) содержат нелинейные зависимости
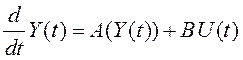 ,
(5.31)
,
(5.31)
![]() ,
(5.32)
,
(5.32)
где ![]() –
– ![]() ‑мерный вектор;
‑мерный вектор; ![]() –
– ![]() ‑мерная нелинейная функция;
‑мерная нелинейная функция; ![]() –
– ![]() ‑мерный
вектор;
‑мерный
вектор; ![]() –
– ![]() ‑мерная
нелинейная функция.
‑мерная
нелинейная функция.
Выполним линеаризацию
уравнений (5.31) и (5.32) в точке оценки ![]() .
.
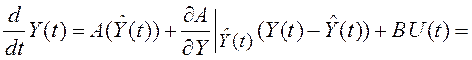
 , (5.33)
, (5.33)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.