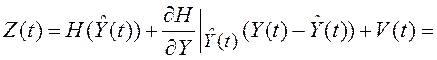
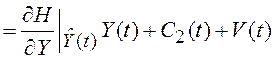 , (5.34)
, (5.34)
где ![]() и
и ![]() – известные величины;
– известные величины;  ;
; 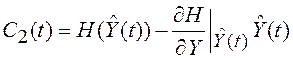 ;
производная нелинейной
;
производная нелинейной ![]() ‑мерной функции
‑мерной функции ![]() по
по ![]() -мерному
вектору
-мерному
вектору ![]() – матрица размером
– матрица размером ![]() ;
;
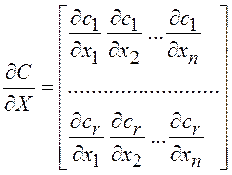 .
.
Можно
привести уравнение (5.34) к виду (5.13), если ввести новую переменную ![]() . Тогда для линейных уравнений (5.33) и
(5.34) алгоритм формирования несмещенной оценки в соответствии (5.14) принимает
вид
. Тогда для линейных уравнений (5.33) и
(5.34) алгоритм формирования несмещенной оценки в соответствии (5.14) принимает
вид
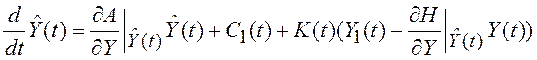 . (5.35)
. (5.35)
Подставим ![]() ,
, ![]() и
и ![]() в (5.35) и получим так называемый
расширенный фильтр Калмана.
в (5.35) и получим так называемый
расширенный фильтр Калмана.
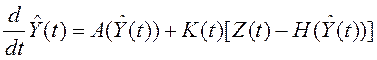 , (5.36)
, (5.36)
где 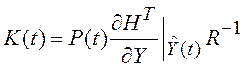 ;
;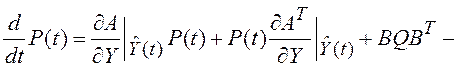
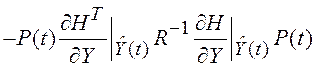
![]() .
.
Линеаризация нелинейных
зависимостей, используемая при построении расширенного фильтра Калмана,
основана на предположении о малой величине ошибки фильтрации. Например, при
линеаризации функции ![]() в уравнении (5.34) величина
ошибки определения временного положения сигнала в дальномере с импульсным
сигналом должна быть малой по сравнению с длительностью импульса.
в уравнении (5.34) величина
ошибки определения временного положения сигнала в дальномере с импульсным
сигналом должна быть малой по сравнению с длительностью импульса.
Пример 5.3. Построим
расширенный фильтр Калмана для дальномера с импульсным сигналом. Случайное
изменение задержки ![]() формируется фильтром, в котором
скорость
формируется фильтром, в котором
скорость ![]() моделируется винеровским процессом. Вектор
состояния системы
моделируется винеровским процессом. Вектор
состояния системы ![]() . Дифференциальное уравнение
процесса в данном примере линейное вида (5.12) с матрицами
. Дифференциальное уравнение
процесса в данном примере линейное вида (5.12) с матрицами ![]() и
и ![]() из
выражения (3.25).
из
выражения (3.25).
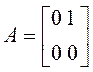 и
и 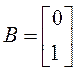 .
.
Уравнение наблюдения в данном случае скалярное.
![]() ,
,
где ![]() –
импульсный сигнал, задержанный на интервал
–
импульсный сигнал, задержанный на интервал ![]() ;
; ![]() белый шум со спектральной плотностью
белый шум со спектральной плотностью ![]() .
.
Найдем производную
нелинейной функции ![]() по
по ![]() в точке
в точке
![]() .
.
Производная содержит две
строки. Вторая строка равна нулю, так как в функции ![]() не
содержится скорость
не
содержится скорость ![]() .
.
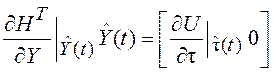 .
.
Используя формулы (5.36), найдем оптимальный коэффициент усиления и уравнение фильтра.
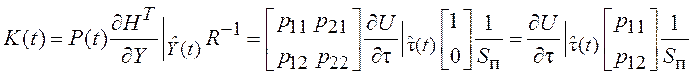 и
и
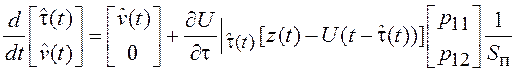 . (5.37)
. (5.37)
Рассмотрим
выражение 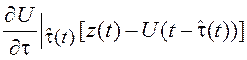 .
.
Построим
осциллограммы сигналов ![]() ,
, 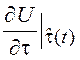 и
и ![]() (рис. 5.11). Результат умножения сигнала
(рис. 5.11). Результат умножения сигнала ![]() на производную зависит от ошибки
оценивания
на производную зависит от ошибки
оценивания ![]() . При отсутствии ошибки
. При отсутствии ошибки ![]() , и произведение представляет симметричную
знакопеременную функцию, которая при интегрировании даст нулевой результат. При
появлении ошибки функция становится несимметричной и появляется сигнал ошибки.
Произведение производной на сигнал
, и произведение представляет симметричную
знакопеременную функцию, которая при интегрировании даст нулевой результат. При
появлении ошибки функция становится несимметричной и появляется сигнал ошибки.
Произведение производной на сигнал ![]() дает симметричную
функцию, и не создает сигнал ошибки. При построении структурной схемы фильтра в
соответствии с выражением (5.37) эту величину не учитываем. Схема оптимального
нелинейного фильтра содержит умножитель принятого сигнала
дает симметричную
функцию, и не создает сигнал ошибки. При построении структурной схемы фильтра в
соответствии с выражением (5.37) эту величину не учитываем. Схема оптимального
нелинейного фильтра содержит умножитель принятого сигнала ![]() на производную
на производную ![]() (рис. 5.12). Эта операция выполняет
функцию оптимального дискриминатора. Сигнал ошибки после умножителя поступает
на сглаживающий фильтр с двумя интеграторами и оптимальными коэффициентами
(рис. 5.12). Эта операция выполняет
функцию оптимального дискриминатора. Сигнал ошибки после умножителя поступает
на сглаживающий фильтр с двумя интеграторами и оптимальными коэффициентами ![]() и
и ![]() .
.
Рассмотрим задачу
нелинейной фильтрации в дискретном времени. Нелинейные разностные уравнения
случайного процесса ![]() и наблюдения
и наблюдения ![]() отличаются от линейных уравнений (5.19) и
(5.20) из-за наличия нелинейных функций
отличаются от линейных уравнений (5.19) и
(5.20) из-за наличия нелинейных функций ![]() размерности
размерности
![]() и
и ![]() и
размерности
и
размерности ![]() .
.
![]() ,
(5.38)
,
(5.38)
![]() .
(5.39)
.
(5.39)
Характеристики шумов ![]() и
и ![]() не
отличаются от линейного случая.
не
отличаются от линейного случая.
Как и ранее в линейной
задаче предполагается наличие известной оптимальной оценки ![]() и ее корреляционной матрицы
и ее корреляционной матрицы ![]() .
.
Выполним линеаризацию
уравнения (5.38) в точке ![]() .
.
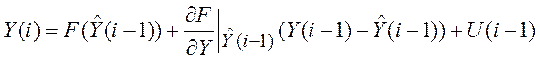 =
=
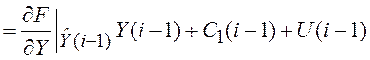 ,
(5.40)
,
(5.40)
где ![]() –
известная величина;
–
известная величина; 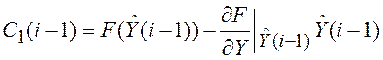 ; производная
; производная ![]() – матрица размером
– матрица размером ![]() ;
;
Используя линейное уравнение (5.40),
найдем оценку экстраполяции 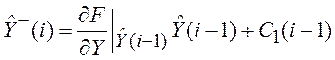 .
.
Выполняя подстановку
величины ![]() , получим выражение.
, получим выражение.
![]() .
(5.41)
.
(5.41)
Для вычисления
корреляционной матрицы ошибок экстраполяции используем выражение подобное
(5.22), заменив ![]() на
на 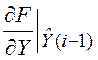 .
.
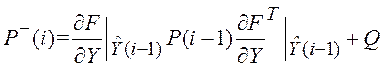 .
(5.42)
.
(5.42)
Теперь выполним
линеаризацию уравнения (5.39) в точке ![]() .
.
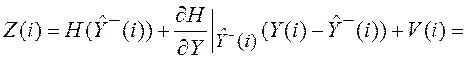
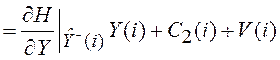 ,
(5.43)
,
(5.43)
где 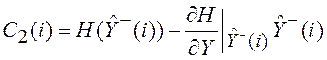 ;
; 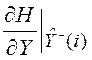 – матрица размером
– матрица размером ![]() .
.
Используя (5.43),
составим наблюдение ![]() , и воспользуемся уравнением
линейной фильтрации (5.23).
, и воспользуемся уравнением
линейной фильтрации (5.23).
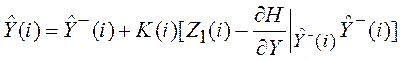 .
.
Выполняя подстановку величины
![]() , получим выражение
, получим выражение
![]() . (5.44)
. (5.44)
Для расчета коэффициента ![]() и корреляционной матрицы ошибок фильтрации
и корреляционной матрицы ошибок фильтрации
![]() используем выражения (5.26) и (5.27),
заменив в них
используем выражения (5.26) и (5.27),
заменив в них ![]() на
на 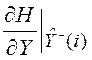 .
.
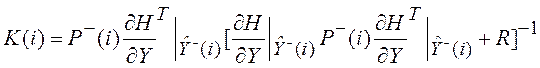 .
(5.45)
.
(5.45)
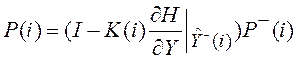 .
(5.46)
.
(5.46)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.