Оптимизация систем радиоавтоматики. Комплексные системы радиоавтоматики, страница 2

Уравнение (5.4) имеет первый порядок, а вектор состояния  модели движения имеет размерность два. Чтобы использовать результаты раздела 3.9, приведем выражение (5.4) к виду (3.46). Для этого введем вектор  при начальном условии  и коэффициент . Тогда состояние  и  в системе действует лишь один интегратор, то есть . Проектируемая система (5.4)  в данном случае является субоптимальной, и оптимизация коэффициента усиления  по минимуму ошибки фильтрации или экстраполяции дает различные результаты. Выполним оптимизацию по минимуму ошибки экстраполяции, используя дисперсионное уравнение (3.49). Полагаем, что при  дисперсия ошибки стремится к стационарному значению, и .

                      (5.5)

Матричное уравнение (5.5) эквивалентно системе из трех алгебраических уравнений (матрица  симметрическая).

,                                      (5.6)

, .

Последовательно вычисляя неизвестные значения элементов матрицы , получим выражение для дисперсии ошибки экстраполяции.

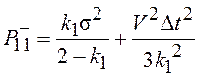.                                          (5.7)

Дифференцируя  из (5.7) по  и приравнивая результат нулю, получим алгебраическое уравнение третьей степени

 или , где .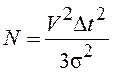

Решение алгебраического уравнения дает оптимальное значение

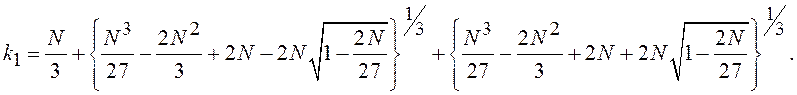            Из решения для непрерывной системы (5.2), используя соотношение , можно получить приближенное значение для дискретной системы . Исследование зависимости   от параметра  показывает, что приближенное (график 1 на рис. 5.3) и точное решение (график 2) практически совпадают при значениях .

            Система с двумя дискретными интеграторами задается системой из двух разностных уравнений, подобных (4.13).

где ; ; .

Для моделирования процесса с ускорением необходим формирующий фильтр с тремя интеграторами, имеющий переходную матрицу (3.30).

,

,

где ;;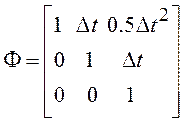; начальное значение ускорения является случайной величиной c нулевым средним и среднеквадратическим значением ; ; дисперсия шума  равна .

          Для нахождения стационарного решения составим дисперсионное уравнение, подобное (5.5). Вектор  , а матрица  имеет размерность . Проектируемый фильтр в данном случае также является субоптимальным, и результат зависит от способа оптимизации. При высоком порядке модели аналитическое решение затруднено, и необходимо использовать численное решение. На рис. 5.4 показаны два варианта выбора коэффициента усиления  в зависимости от величины .

Значения  от выбора варианта оптимизации практически не зависят.  Штриховая линия соответствует оптимизации по минимуму дисперсии ошибок фильтрации, непрерывная – экстраполяции. Для сравнения штрих-пунктиром показаны результаты приближенного расчета по формулам, полученным из непрерывного расчета (5.3).

 и .

            Сравнение результатов численного расчета с приближенным показывает, что при  целесообразно использовать упрощенный метод расчета.

5.3. Синтез оптимальных следящих систем с постоянными параметрами

При проектировании следящих измерителей желательна не только оптимизация параметров, но и выбор оптимальной структуры. Задача оптимальной линейной фильтрации заключается в построении фильтра, вырабатывающего путем линейного преобразования наблюдения  оценку  с минимальной среднеквадратичной ошибкой  разности  выходного сигнала фильтра и желаемого выхода , формируемого некоторым линейным преобразованием  (рис. 5.5). Впервые такая задача была сформулирована в 1939 году академиком А.Н. Колмогоровым. Затем в 1949 году американским ученым Н. Винером был найден физически реализуемый оптимальный линейный фильтр.

            Если положить для простоты , то весовая функция оптимального фильтра  определяется решением интегрального уравнения Винера-Хопфа

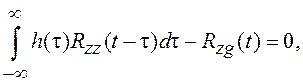
 ,                              (5.8)

где  ; ; .

            Отметим, что при составлении уравнения (5.8) используются только корреляционные функции процессов, но не используются их распределения. При любом виде распределений полученный фильтр является оптимальным в классе линейных фильтров. Однако для негауссовских процессов возможно улучшение оценки путем нелинейной обработки.