Оптимизация систем радиоавтоматики. Комплексные системы радиоавтоматики, страница 13

В качестве примера выше рассматривалось движение самолета, однако уравнения (6.14) и (6.21) можно использовать для описания движения центра масс любого транспортного средства. Первые комплексные системы использовались в навигационных комплексах самолетов, но в настоящее время в связи с широким использованием глобальной навигационной системы и появлением миниатюрных ИНС комплексирование используется и в навигационных системах наземного транспорта.

При вычислительной реализации комплексной фильтрации целесообразно использовать дискретное время и описание системы с помощью разностных уравнений. Составление таких уравнений было выполнено для процесса с экспоненциально-коррелированной скоростью в разделе 3.8. Уравнения (6.21) отличаются от уравнений (3.34) знаком скорости  и наличием известной величины  в правой части первого уравнения. Поэтому система разностных уравнений имеет вид:

; ,         (6.23)

а переходная матрица системы отличается от матрицы, даваемой выражением (3.35), знаком . В векторной записи система (6.23) имеет вид:

,                                             (6.24)

где ; ; ;  ; .

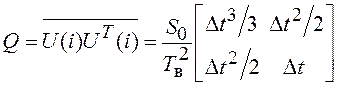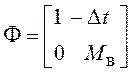Наблюдение в дискретном времени имеет вид:

,                                        (6.25)

где ;  – дискретный белый шум с известной дисперсией.

6.6. Комплексирование дальномерной навигационной системы, датчика скорости и курсовой системы

            Построим комплексный фильтр для дальномерной навигационной системы, предназначенной для определения координат самолета. Реальная система отличается от рассмотренной дальномерной системы в примере 5.3 тем, что измерение дальностей выполняется последовательно во времени c помощью одного приемника (рис. 6.7, а).  Одновременное измерение всех дальностей требует применения нескольких приемников, так как радиомаяки работают на различных частотах. При последовательном измерении используется один приемник, измеряющий поочередно дальности выбранных радиомаяков с периодом несколько секунд (рис. 6.7, б). Для снижения ошибок определения координат, возникающих из-за прерывистого приема данных, используем комплексирование с автономными средствами. Скорость измеряется датчиком воздушной скорости. Чтобы получить проекции вектора воздушной скорости  на оси  и , необходимо также измерять угол курса .

            Строим систему на основе принципа инвариантности и используем уравнения (6.23). При измерении положения самолета на плоскости составляем две идентичные системы уравнений – для координат  и . Для простоты полагаем, что системы независимые.

        ; ;

;  , (6.26)

где  и  – координаты;  и  – соответствующие проекции вектора воздушной скорости ;  и  – ошибки измерения скорости;  и  – некоррелированные дискретные белые шумы.

            Система уравнений (6.26) в векторном представлении составляется из элементов и матриц  выражения (6.24).

; ; , при этом

; .

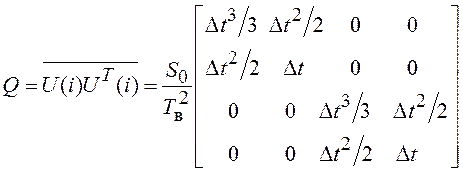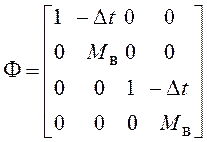            Уравнение наблюдения отличается от уравнения (5.46) из-за того, что используется последовательный прием сигналов радиомаяков.

,                                     (6.27)

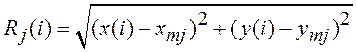где  – скалярная функция; ;  – номер радиомаяка; ;  – дискретный белый шум с дисперсией .

            Производная нелинейной функции  в точке  в отличие от (5.47) вычисляется только для измерения-того радиомаяка.

.

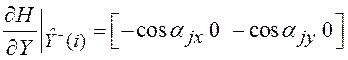            Используя результаты раздела 5.6, составим уравнения расширенного фильтра Калмана:

1.  Уравнение экстраполяции .

2.  Расчет матрицы ошибок экстраполяции .

3.  Расчет коэффициента усиления .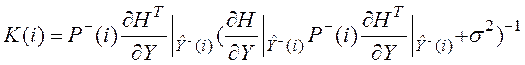

4.  Уравнение фильтрации .                  (6.28)

5.  Расчет матрицы ошибок фильтрации .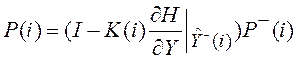

Алгоритм строится в предположении, что известна оценка  и

матрица . В начальный момент  необходимо иметь априорные  данные о координатах  и дисперсиях их ошибок. Составим уравнения экстраполяции, используя (6.26).

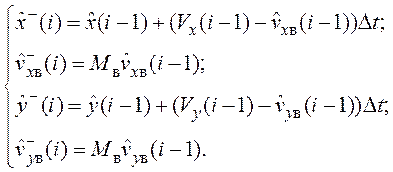                                             (6.29)

Коэффициент усиления  в уравнении фильтрации (6.28) представляет собой вектор . Коэффициент усиления  необходимо вычислять в каждый момент времени , так как его значение зависит от значения оценки  .

Вычислим разность

 .          (6.30)

Тогда из уравнения фильтрации (6.28) получим систему уравнений: