Оптимизация систем радиоавтоматики. Комплексные системы радиоавтоматики, страница 12

            Рассмотрим использование информации о движении объекта на примере определения одной из координат (дальности) самолета. Составим систему уравнений, описывающих движение самолета и измерение скорости и положения с помощью датчика воздушной скорости и дальномера  (рис. 6.6, а). Для моделирования движения самолета с ускорением в виде экспоненциально-коррелированного процесса используем уравнения (3.38).

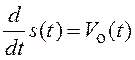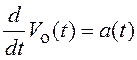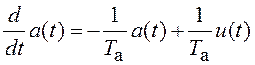; ; ,                   (6.14)

где ,  и  – путь, скорость и ускорение;  – интервал корреляции ускорения;  – белый гауссовский шум со спектральной плотностью .

            Ошибка датчика скорости, создаваемая ветром, является медленно изменяющейся величиной из-за изменения погодных условий вдоль трассы полета самолета. Эта ошибка моделируется как экспоненциально-коррелированный процесс, определяемый уравнением вида (3.31).

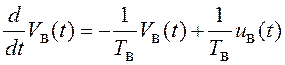,                                          (6.15)

где  – ошибка, создаваемая ветром;  – постоянная времени;  – белый гауссовский шум со спектральной плотностью .

            Система дифференциальных уравнений модели воздействия содержит выражения (6.14) и (6.15), а вектор состояния имеет вид . Векторная форма системы дифференциальных уравнений имеет вид:

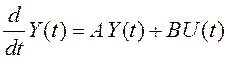,                                          (6.16)

где ; ; .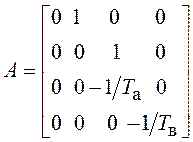

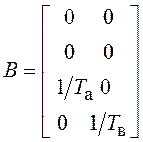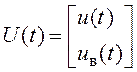            Измерение скорости  выполняется датчиком воздушной скорости с ошибкой , а уравнение наблюдения имеет вид:

.                                                   (6.17)

            Измерение пройденного пути  производится радиодальномером с ошибкой , которая является белым шумом  со спектральной плотностью .

.                                                  (6.18)

Вектор наблюдения  имеет вид

,                                            (6.19)

где ; ; .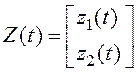

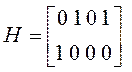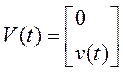            Оптимальное объединение данных в комплексной системе затем сводится к  построению фильтра Калмана для оценивания вектора состояния  по наблюдению .

            Размер вектора состояния  в рассмотренном примере равен числу дифференциальных уравнений – 4. Но в примере рассматривается движение только по одной координате. При моделировании движения на плоскости число уравнений возрастет до 8, а в трехмерном пространстве – до 12.

Используем принцип инвариантности для упрощения полученной комплексной системы. Воспользуемся методом компенсации для модели воздействия, рассмотренной в предыдущем примере. В схеме компенсации формируется сигнал , не зависящий от скорости движения самолета  (рис. 6.6, б). Для этого из радиотехнического измерения  вычитается интеграл воздушной скорости . Используя (6.17) и (6.18), получим

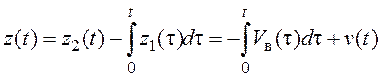.                              (6.20)

Из выражения (6.20) следует, что величина  зависит только от ошибки измерения скорости. Далее необходимо построить фильтр, выполняющий оптимальную оценку ошибки, создаваемой ветром. 

Построим модель воздействия, не содержащего скорость самолета. Ошибка датчика воздушной скорости  моделируется как экспоненциально-коррелированный процесс с помощью выражения (6.12).

Преобразуем величину  так, чтобы исключить скорость объекта .

.

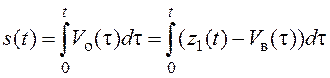            Тогда при использовании принципа инвариантности система уравнений модели воздействия содержит два уравнения:

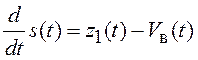 и 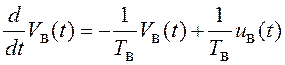.                 (6.21)

            Система уравнений (6.21) в векторной форме имеет вид:

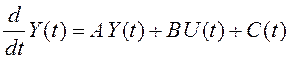,                                                   (6.22)

где ;  ; ; ; .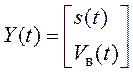

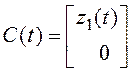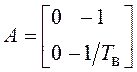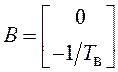Вектор  содержит известную величину – измерение датчика воздушной скорости. В векторе наблюдения  в выражении (6.19) остается только измерение дальномера .

Несмотря на то, что ускорение и скорость самолета отсутствуют в уравнениях (6.21), величина пути  зависит от истинной скорости , так как разность воздушной скорости и случайной ошибки .

Использование принципа инвариантности снизило размер вектора состояния  до двух элементов (вместо четырех) и устранило зависимость от априорных данных о движении объекта.