Оптимизация систем радиоавтоматики. Комплексные системы радиоавтоматики, страница 9

Выражение (6.1) можно представить как результат использования двух фильтров  с ПФ  и . Тогда схема компенсации может быть заменена эквивалентной схемой фильтрации.

.

В схеме фильтрации ПФ для полезного параметра  , и эта схема обладает инвариантностью по отношению к изменению полезного параметра. Можно обобщить принцип фильтрации на случай комплексирования  источников информации .

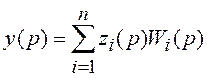,   где 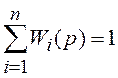.                                  (6.2)

В качестве фильтров в схеме фильтрации могут применяться следящие измерители. При этом для получения различных ПФ можно использовать различные входы одной и той же следящей системы.

Ниже рассматривается ряд примеров использования принципа инвариантности.

6.3. Комплексирование измерителей задержки сигналов

Рассмотрим пример комплексирования со слабой интеграцией различных источников информации при измерении задержки сигнала спутниковой навигационной системы. В аппаратуре потребителя имеется измеритель задержки принятого кодированного сигнала. Устройство этого измерителя рассмотрено в 4.3. Недостатком этого измерителя является большая флюктуационная  ошибка.

Измеренное значение задержки сигнала в кодовом канале  имеет вид

,

где  – истинное значение задержки;  – случайная ошибка.

 С другой стороны в аппаратуре потребителя имеется система фазовой автоподстройки частоты, необходимая для приема информационных сообщений спутника. В  примерах 4.2 и 4.3 (раздел 4.10) показано, что точность измерения временного положения сигнала в фазовом канале намного выше, чем в кодовом. Однако использование фазовой информации затрудняется из-за наличия ошибки неоднозначности фазового отсчета. Измеренное значение задержки сигнала в фазовом канале  равно

,

где  – случайная ошибка;   – ошибка неоднозначности фазового отсчета;  – длина волны;  – скорость света.

 Величина случайной ошибки в фазовом канале пренебрежимо мала по сравнению с ошибкой кодового канала. Поэтому при комплексировании предполагаем, что имеется источник информации  с большой случайной ошибкой  и источник  с постоянной ошибкой . Используем схему фильтрации, в которой сигнал  поступает на фильтр нижних частот и сигнал  – на фильтр верхних частот (рис.6.4). В качестве фильтров используем -цепи с постоянной времени  и ПФ

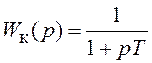 (ФНЧ) и  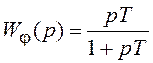 (ФВЧ).                               (6.3)

Сумма этих ПФ равна единице.

Пример 6.1. Оценим полезный эффект комплексирования в авиационной аппаратуре потребителя. В соответствии с международными стандартами для аппаратуры гражданской авиации постоянная времени фильтра выбирается равной с. Фильтр нижних частот можно реализовать с помощью системы с одним интегратором, имеющей коэффициент усиления . Тогда полоса пропускания фильтра нижних частот  равна  (табл. 3.2). При частоте поступления данных 1 Гц (=1с) СПМ шума кодового канала равна  [], где из примера 4.2 м. Таким образом, на выходе ФНЧ получим среднеквадратическое значение ошибки измерения задержки 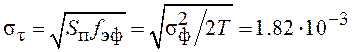  мкс или в единицах расстояния м. Флюктуационная ошибка фазового канала проходит через ФВЧ без ослабления, но ее величина пренебрежимо мала (0.677см в примере 4.3). Таким образом комплексирование данных позволило снизить величину среднеквадратического значения ошибки измерения дальности в 14 раз.

Построим цифровой алгоритм комплексирования, реализующий фильтры (6.3). ПФ ФНЧ  соответствует апериодическому звену, которое может быть реализовано в виде системы с одним интегратором с ПФ  . Дифференциальное уравнение для состояния такой системы  используем из примера 3.4.

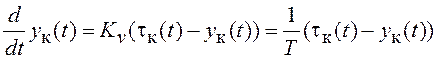.                      (6.4)

ПФ ФВЧ , и может быть реализована путем дифференцирования сигнала, умножения его на коэффициент  и обработки в фильтре с ПФ . При составлении дифференциального уравнения состояния ФВЧ  возьмем уравнение (6.4) и вместо входного сигнала  подставим производную .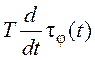

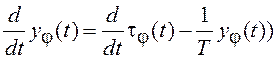.                                                 (6.5)       

Оценка задержки  является суммой  и . Тогда сложив (6.4) и (6.5) получим уравнение:

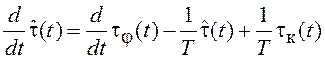.                                          (6.6)