Проектирование реконструкции железной дороги: Методические указания к курсовому проектированию, страница 9

Тогда Х_ск=126,40 м, Y_ск=2,25 рад. Далее (рис. 3.4) показана схема подбора радиуса проектной круговой кривой.

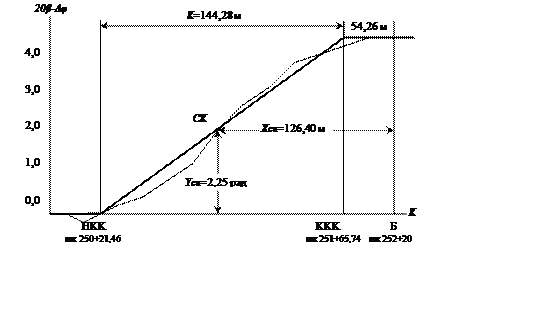Рис.3.4.  Угловые диаграммы существующей и

проектной кривых

Важное замечание: Х_ск откладывают справа налево от точки Б. Тогда пикет точки СК равен:   пк СК=пкБ-Х_ск.

В примере – пк СК=пк 252+20,00 – 126,40=пк 250+93,60.

Порядок подбора радиуса:

- провести через точку СК прямую, по возможности ближе к угловой диаграмме существующей кривой, и графически определить длину круговой кривой (см. рис. 3.4); пусть, например, К=145 м;

- определить радиус этой кривой R=K/φ=145/0,22544 =
= 643,18 м;

- принято округлять радиус до величины, кратной 1, 5 или 10 м, в примере  величина проектного радиуса принята равной 640 м; теперь длина круговой равна

K=R·φ=640·0,22544=144,28 м.

Пикет начала круговой кривой

пк НКК=пк СК-К/2=пк 250+93,60-144,28/2=пк 250+21,46.

Пикет конца кривой

пк ККК=пк НКК+К=пк 250+21,46+144,28=пк 251+65,74.

Шаг 3. Основная проверка: площади углограмм существующей и проектной кривых должны быть равны. Только в этом случае будет выполнено обязательное условие: сдвижка в точке Б (см.рис.3.4) равна нулю.

Площадь угловой диаграммы проектной кривой Ω_п состоит из площадей треугольника, основание которого – длина проектной круговой кривой, а высота – угол  кривой в рад., и прямоугольника, высота которого равна углу кривой, а основание – разности пикетов точки Б и конца кривой:

Ω_п = К·φ/2+(пк Б-пк ККК)·φ

В условиях примера:  Ω_п = 144,28·0,22544/2+54,26·0,22544 = 28,495

Результат на 0,005 не совпадает с площадью углограммы существующей кривой, что приемлемо, так как связано с  округлениями при расчетах.

Шаг 4. Определение площади угловой диаграммы на всех точках деления кривой и сдвижек от круговой кривой. Расчет удобно выполнять в Excel (табл.3.4).

Таблица 3.4

Определение площади угловой диаграммы проектной кривой

и сдвижек от выправки круговой кривой

A	B	C	D	E	F	G	H
Пикет,+	k1 (м)	ω1	k2 (м)	ω2	ω1+ω2=ωп	ωс	∆=ωп-ωс
249,8000	0	0	0	0	0,000	0,000	0,000
250,0000	0	0	0	0	0,000	-0,012	0,012
250,2000	0	0	0	0	0,000	0,196	-0,196
250,2146	0	0	0	0	0,000
250,4000	18,54	0,269	0	0	0,269	0,603	-0,334
250,6000	38,54	1,160	0	0	1,160	1,458	-0,298
250,8000	58,54	2,677	0	0	2,677	3,054	-0,377
251,0000	78,54	4,819	0	0	4,819	5,238	-0,419
251,2000	98,54	7,586	0	0	7,586	8,095	-0,509
251,4000	118,54	10,978	0	0	10,978	11,489	-0,511
251,6000	138,54	14,995	0	0	14,995	15,416	-0,421
251,6574	144,28	16,263	0	0	16,263
251,8000			14,26	19,478	19,478	19,635	-0,157
252,0000			34,26	23,987	23,987	24,002	-0,015
252,2000			54,26	28,495	28,495	28,490	0,005

В столбцах указаны:

A – пикеты и плюсы точек деления с включением пикетов НКК и ККК; 

В – нули до НКК включительно, далее расстояния k₁ от НКК до ККК,  k₁=(пикет точки – пк НКК)·100;